Свертка

Свертка - это корреляционная функция f (τ) с обращенной функцией g (t-τ).

Оператор свертки - это символ звездочки * .

Свертка f (t) и g (t) равна интегралу от f (τ), умноженного на f (t-τ):

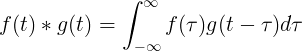
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Свертка двух дискретных функций определяется как:

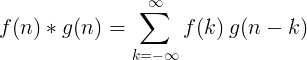
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

Двумерная дискретная свертка обычно используется для обработки изображений.

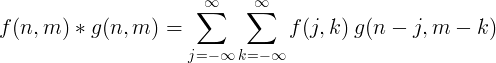
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: г (ндж, мк)$

Мы можем фильтровать дискретный входной сигнал x (n) путем свертки с импульсной характеристикой h (n), чтобы получить выходной сигнал y (n).

у ( п ) = х ( п ) * ч ( п )

Преобразование Фурье умножения 2 функций равно свертке преобразований Фурье каждой функции:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Преобразование Фурье свертки 2 функций равно умножению преобразований Фурье каждой функции:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Смотрите также