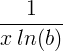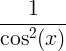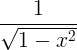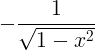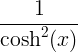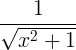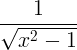Производные правила
Производные правила и законы. Таблица производных функций.
Производное определение
Производная функции - это отношение разности значений функции f (x) в точках x + Δx и x к Δx, когда Δx бесконечно мало. Производная - это наклон функции или наклон касательной в точке x.
![]()
Вторая производная
Вторая производная определяется по формуле:
![]()
Или просто выведите первую производную:
![]()
N-я производная
Производная n вычисляется путем вычисления f (x) n раз.
В п - е производная равна производной от (п-1) производное:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Пример:
Найдите четвертую производную от
е ( х ) = 2 х 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Производная на графике функции
Производная функции - это наклон касательной прямой.
Производные правила
| Правило производной суммы | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Правило производного продукта | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Правило производного частного | 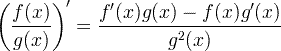 |
| Правило производной цепочки | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Правило производной суммы
Когда a и b постоянные.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Пример:
Найдите производную от:
3 х 2 + 4 х.
Согласно правилу сумм:
а = 3, б = 4
е ( х ) = х 2 , g ( х ) = х
f ' ( x ) = 2 x , g' ( x ) = 1
(3 х 2 + 4 х ) '= 3⋅2 х + 4⋅1 = 6 х + 4
Правило производного продукта
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Правило производного частного
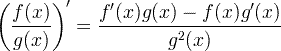
Правило производной цепочки
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Это правило можно лучше понять с помощью обозначений Лагранжа:
![]()
Функция линейной аппроксимации
Для малых Δx мы можем получить приближение к f (x 0 + Δx), когда мы знаем f (x 0 ) и f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Таблица производных функций
| Название функции | Функция | Производная |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Постоянный | const |
0 |
| Линейный | х |
1 |
| Сила | х а |
топор а- 1 |
| Экспоненциальный | e x |
e x |
| Экспоненциальный | а х |
a x ln a |
| Натуральный логарифм | ln ( x ) |
|
| Логарифм | журнал b ( x ) |
|
| Синус | грех х |
cos x |
| Косинус | cos x |
-sin x |
| Касательная | загар х |
|
| Арксинус | arcsin x |
|
| Арккосин | arccos x |
|
| Арктангенс | arctan x |
|
| Гиперболический синус | зп х |
cosh x |
| Гиперболический косинус | cosh x |
зп х |
| Гиперболический тангенс | tanh x |
|
| Обратный гиперболический синус | sh -1 x |
|
| Обратный гиперболический косинус | cosh -1 x |
|
| Обратный гиперболический тангенс | танх -1 х |
|
Производные примеры
Пример # 1
е ( х ) = х 3 +5 х 2 + х +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Пример # 2
е ( х ) = грех (3 х 2 )
При применении цепного правила:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Тест второй производной
Когда первая производная функции равна нулю в точке x 0 .
f '( x 0 ) = 0
Тогда вторая производная в точке x 0 , f '' (x 0 ), может указывать на тип этой точки:
| f '' ( x 0 )/ 0 |
местный минимум |
| f '' ( х 0 ) <0 |
локальный максимум |
| f '' ( х 0 ) = 0 |
неопределенный |
Смотрите также
ИСЧИСЛЕНИЕ
- Предел
- Производная
- интеграл
- Серии
- Преобразование Лапласа
- Свертка
- Символы исчисления
БЫСТРЫЕ ТАБЛИЦЫ