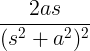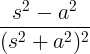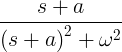Преобразование Лапласа

Преобразование Лапласа преобразует функцию временной области в функцию s-области путем интегрирования от нуля до бесконечности

функции во временной области, умноженной на e ^-st .

Преобразование Лапласа используется для быстрого поиска решений дифференциальных уравнений и интегралов.

Вывод во временной области преобразуется в умножение на s в s-области.

Интеграция во временной области трансформируется в деление на s в s-области.

Функция преобразования Лапласа

Преобразование Лапласа определяется оператором L {}:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Обратное преобразование Лапласа можно вычислить напрямую.

Обычно обратное преобразование дается из таблицы преобразований.

Название функции	Функция во временной области	Преобразование Лапласа
Название функции	f ( t )	F ( s ) = L { f ( t )}
Постоянный	1	$\ frac {1} {s}$
Линейный	т	$\ frac {1} {s ^ 2}$
Сила	т ^н	$\ гидроразрыва {п!} {s ^ {n + 1}}$
Сила	т ^а	Γ ( a +1) ⋅ s ^{- ( a +1)}
Экспонента	е ^в	$\ frac {1} {sa}$
Синус	грешить на	$\ гидроразрыва {а} {s ^ 2 + a ^ 2}$
Косинус	потому что в	$\ гидроразрыва {s} {s ^ 2 + a ^ 2}$
Гиперболический синус	грех в	$\ frac {a} {s ^ 2-a ^ 2}$
Гиперболический косинус	пижон в	$\ frac {s} {s ^ 2-a ^ 2}$
Растущий синус	т грех в	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Растущий косинус	t cos в	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Затухающий синус	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Затухающий косинус	е ^-при соз ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Дельта-функция	δ ( t )	1
Отложенная дельта	δ ( та )	e ^-as

Имя свойства	Функция во временной области	Преобразование Лапласа	Комментарий
	f ( t )	F ( s )
Линейность	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b постоянны
Изменение масштаба	f ( at )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	а / 0
сдвиг	е ^-при е ( т )	F ( s + a )
Задержка	f ( ta )	e ^{- как} F ( s )
Вывод	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-я производная	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Сила	т ^н ф ( т )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Интеграция	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Взаимный	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Свертка	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* - оператор свертки
Периодическая функция	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$