е постоянная

Константа или число Эйлера - математическая константа. Константа е - действительное и иррациональное число.

е = 2,718281828459 ...

Определение слова e
Свойства е
Основание е логарифм
Экспоненциальная функция
Формула Эйлера

Определение слова e

Константа e определяется как предел:

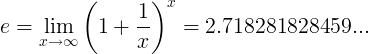
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2,718281828459 ...$

Альтернативные определения

Константа e определяется как предел:

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

Константа e определяется как бесконечный ряд:

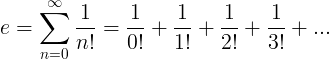
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Свойства е

Взаимно от е

Обратное к e является пределом:

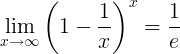
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

Производные e

Производная экспоненциальной функции - это экспоненциальная функция:

( e ^x ) '= e ^x

Производная функции натурального логарифма является обратной функцией:

(log _e x ) '= (ln x )' = 1 / x

Интегралы от e

Неопределенный интеграл от экспоненциальной функции e ^x является экспоненциальной функцией e ^x .

∫ е ^х dx = е ^х + с

Неопределенный интеграл функции натурального логарифма log _e x равен:

∫ журнал _e x dx = ∫ ln x dx = x ln x - x + c

Определенный интеграл от 1 до e обратной функции 1 / x равен 1:

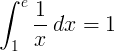
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Основание е логарифм

Натуральный логарифм числа x определяется как логарифм числа x по основанию e:

ln x = журнал _e x

Экспоненциальная функция

Экспоненциальная функция определяется как:

е ( х ) = ехр ( х ) = е ^х

Формула Эйлера

Комплексное число e ^iθ имеет тождество:

е ^iθ = cos ( θ ) + i sin ( θ )

i - мнимая единица (квадратный корень из -1).

θ - любое действительное число.