Нулевое число (0)
- Определение нулевого числа
- История нулевых номеров
- Свойства с нулевым числом
- Наборы, содержащие ноль
Определение нулевого числа
Ноль - это число, используемое в математике для обозначения отсутствия количества или нулевого количества.
Когда на столе 2 яблока и мы берем 2 яблока, мы можем сказать, что на столе нет яблок.
Нулевое число не является положительным и отрицательным числом.
Ноль также является цифрой-заполнителем в других числах (например: 40,103, 170).
Ноль - это число?
Ноль - это число. Это не положительное или отрицательное число.
Нулевая цифра
При написании чисел нулевая цифра используется в качестве заполнителя.
Например:
204 = 2 × 100 + 0 × 10 + 4 × 1
История нулевых номеров
Кто придумал нулевое число?
Современный символ 0 был изобретен в Индии в VI веке, позже использовался персами и арабами, а затем и в Европе.
Символ нуля
Нулевое число обозначается символом 0 .
В арабской системе счисления используется символ ٠.
Свойства с нулевым числом
x представляет любое число.
| Операция | Правило | пример |
|---|---|---|
Дополнение |
х + 0 = х |
3 + 0 = 3 |
Вычитание |
х - 0 = х |
3 - 0 = 3 |
Умножение |
х × 0 = 0 |
5 × 0 = 0 |
Деление |
0 ÷ x = 0 , когда x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 не определено |
5 ÷ 0 не определено |
|
Возведение в степень |
0 х = 0 |
0 5 = 0 |
| х 0 = 1 |
5 0 = 1 |
|
Корень |
√ 0 = 0 |
|
Логарифм |
log b (0) не определено |
|
| |
||
Факториал |
0! = 1 |
|
Синус |
грех 0º = 0 |
|
Косинус |
cos 0º = 1 |
|
Касательная |
загар 0º = 0 |
|
Производная |
0 '= 0 |
|
интеграл |
∫ 0 d x знак равно 0 + C |
|
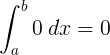 |
Нулевое дополнение
Сложение числа плюс ноль равно числу:
х + 0 = х
Например:
5 + 0 = 5
Нулевое вычитание
Вычитание числа минус ноль равно числу:
х - 0 = х
Например:
5 - 0 = 5
Умножение на ноль
Умножение числа на ноль равно нулю:
х × 0 = 0
Например:
5 × 0 = 0
Число деленное на ноль
Деление числа на ноль не определено:
x ÷ 0 не определено
Например:
5 ÷ 0 не определено
Ноль делится на число
Деление нуля на число равно нулю:
0 ÷ х = 0
Например:
0 ÷ 5 = 0
Число в нулевой степени
Степень числа, возведенного в ноль, равна единице:
х 0 = 1
Например:
5 0 = 1
Логарифм нуля
Логарифм нуля по основанию b не определен:
log b (0) не определено
Нет числа, с которым мы могли бы поднять основание b до нуля.
Только предел логарифма x по основанию b, когда x сходится к нулю, равен минус бесконечности:
![]()
Наборы, содержащие ноль
Ноль - это элемент наборов натуральных, целых, действительных и комплексных чисел:
| Установить | Установить обозначение членства |
|---|---|
| Натуральные числа (неотрицательные) | 0 ∈ ℕ 0 |
| Целые числа | 0 ∈ ℤ |
| Вещественные числа | 0 ∈ ℝ |
| Сложные числа | 0 ∈ ℂ |
| Рациональное число | 0 ∈ ℚ |
Ноль - четное или нечетное число?
Набор четных чисел:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Набор нечетных чисел:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Ноль - это целое число, кратное 2:
0 × 2 = 0
Ноль является членом набора четных чисел:
0 ∈ {2 k , k ∈ℤ}
Итак, ноль - это четное число, а не нечетное.
Ноль - натуральное число?
Есть два определения набора натуральных чисел.
Набор неотрицательных целых чисел:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Набор натуральных чисел:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Ноль является членом набора неотрицательных целых чисел:
0 ∈ ℕ 0
Ноль не входит в набор натуральных чисел:
0 ∉ ℕ 1
Ноль - это целое число?
У целых чисел есть три определения:
Набор целых чисел:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Набор неотрицательных целых чисел:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Набор натуральных чисел:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Ноль является членом набора целых чисел и набора неотрицательных целых чисел:
0 ∈ ℤ
0 ∈ ℕ 0
Ноль не входит в набор натуральных чисел:
0 ∉ ℕ 1
Ноль - это целое число?
Набор целых чисел:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Ноль входит в набор целых чисел:
0 ∈ ℤ
Итак, ноль - это целое число.
Является ли ноль рациональным числом?
Рациональное число - это число, которое можно выразить как частное двух целых чисел:
ℚ = { н / м ; n , m ∈ℤ}
Ноль можно записать как частное двух целых чисел.
Например:
0 = 0/3
Итак, ноль - рациональное число.
Ноль - это положительное число?
Положительное число определяется как число больше нуля:
х / 0
Например:
5/ 0
Поскольку ноль не больше нуля, это не положительное число.
Ноль - простое число?
Число 0 не является простым числом.
Ноль не является положительным числом и имеет бесконечное количество делителей.
Наименьшее простое число - 2.