Дисперсия

В вероятности и статистике дисперсия случайной величины - это среднее значение квадрата расстояния от среднего значения. Он показывает, как случайная величина распределяется около среднего значения. Небольшая дисперсия указывает на то, что случайная величина распределена около среднего значения. Большая дисперсия указывает на то, что случайная величина распределена далеко от среднего значения. Например, при нормальном распределении узкая кривая колокола будет иметь небольшую дисперсию, а широкая кривая колокола будет иметь большую дисперсию.

Определение отклонения

Дисперсия случайной величины X - это ожидаемое значение квадратов разницы X и ожидаемого значения μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Из определения дисперсии мы можем получить

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Дисперсия непрерывной случайной величины

Для непрерывной случайной величины со средним значением μ и функцией плотности вероятности f (x):

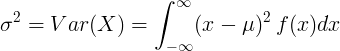
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

или

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Дисперсия дискретной случайной величины

Для дискретной случайной величины X со средним значением μ и функцией массы вероятности P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

или

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

Свойства дисперсии

Когда X и Y являются независимыми случайными величинами:

Вар ( X + Y ) = Вар ( X ) + Вар ( Y )

 

Стандартное отклонение ►

 

Смотрите также

ВЕРОЯТНОСТЬ И СТАТИСТИКА
БЫСТРЫЕ ТАБЛИЦЫ