Распределение вероятностей

В вероятности и статистике распределение является характеристикой случайной величины, описывает вероятность появления случайной величины в каждом значении.

Каждое распределение имеет определенную функцию плотности вероятности и функцию распределения вероятностей.

Хотя существует неопределенное количество распределений вероятностей, используется несколько общих распределений.

Кумулятивная функция распределения
Таблица непрерывных распределений
Таблица дискретных распределений

Кумулятивная функция распределения

Распределение вероятностей описывается кумулятивной функцией распределения F (x),

которая представляет собой вероятность случайной переменной X получить значение, меньшее или равное x:

F ( х ) = Р ( Х ≤ х )

Непрерывное распространение

Кумулятивная функция распределения F (x) вычисляется путем интегрирования функции плотности вероятности f (u) непрерывной случайной величины X.

Дискретное распределение

Кумулятивная функция распределения F (x) вычисляется путем суммирования функции массы вероятности P (u) дискретной случайной величины X.

Таблица непрерывных распределений

Непрерывное распределение - это распределение непрерывной случайной величины.

Пример непрерывного распространения

...

Таблица непрерывных распределений

Название дистрибутива	Символ распределения	Функция плотности вероятности (pdf)	Подлый	Дисперсия
		f _X ( x )	μ = E ( X )	σ ² = Var ( X )
Нормальный / гауссовский	Х ~ N (μ, σ ² )	$\ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}$	μ	σ ²
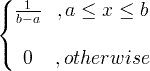Униформа	Х ~ U ( а , Ь )	$\ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, в противном случае \ end {matrix}$		$\ frac {(ba) ^ 2} {12}$
Экспоненциальный	Х ~ ехр (λ)	$\ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix}$	$\ frac {1} {\ lambda}$	$\ frac {1} {\ lambda ^ 2}$
Гамма	Х ~ гамма ( с , λ)	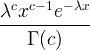$\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}$ х / 0, с / 0, λ/ 0	$\ frac {c} {\ lambda}$	$\ frac {c} {\ lambda ^ 2}$
Площадь Чи	Х ~ х ² ( к )	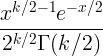$\ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}$	k	2 к
Wishart
F	Х ~ F ( к ₁, к ₂ )
Бета
Weibull
Лог-нормальный	X ~ LN (μ, σ ² )
Рэлей
Коши
Дирихле
Лаплас
Леви
Рис
Студенческий т

Таблица дискретных распределений

Дискретное распределение - это распределение дискретной случайной величины.

Пример дискретного распределения

...

Таблица дискретных распределений

Название дистрибутива	Символ распределения	Вероятностная функция масс (pmf)		Подлый	Дисперсия
		е _х ( к ) = Р ( Х = к ) к = 0,1,2, ...		Е ( х )	Вар ( х )
Биномиальный	X ~ Bin ( n , p )	$\ binom {n} {k} p ^ {k} (1-p) ^ {nk}$		нп	нп (1- п )
Пуассон	X ~ Пуассон (λ)		λ ≥ 0	λ	λ
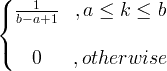Униформа	Х ~ U ( а, Ь )	$\ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, иначе \ end {matrix}$		$\ frac {a + b} {2}$	$\ frac {(b-a + 1) ^ {2} -1} {12}$
Геометрический	X ~ Geom ( p )	$п (1-р) ^ {k}$		$\ frac {1-p} {p}$	$\ frac {1-p} {p ^ 2}$
Гипергеометрический	Х ~ HG ( N , K , n )		N = 0,1,2, ... К = 0,1, .., N п = 0,1, ..., N	$\ frac {nK} {N}$	$\ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}$
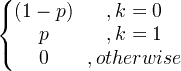Бернулли	X ~ Берн ( р )	$\ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, иначе \ end {matrix}$		p	п (1- п )

Распределение вероятностей

Кумулятивная функция распределения

Непрерывное распространение

Дискретное распределение

Таблица непрерывных распределений

Пример непрерывного распространения

Таблица непрерывных распределений

Таблица дискретных распределений

Пример дискретного распределения

Таблица дискретных распределений

Смотрите также

ВЕРОЯТНОСТЬ И СТАТИСТИКА

БЫСТРЫЕ ТАБЛИЦЫ