Kvadratická rovnica
Kvadratická rovnica je polynóm druhého rádu s 3 koeficientmi - a , b , c .
Kvadratická rovnica je daná vzťahom:
sekera 2 + bx + c = 0
Riešenie kvadratickej rovnice je dané 2 číslami x 1 a x 2 .
Kvadratickú rovnicu môžeme zmeniť na formu:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratický vzorec
Riešenie kvadratickej rovnice je dané kvadratickým vzorcom:
![]()
Výraz vo vnútri druhej odmocniny sa nazýva diskriminačný a je označený Δ:
Δ = b 2 - 4 ac
Kvadratický vzorec s diskriminačným zápisom:
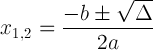
Tento výraz je dôležitý, pretože nám môže povedať o riešení:
- Keď Δ/ 0, existujú 2 skutočné korene x 1 = (- b + √ Δ ) / (2a) a x 2 = (- b-√ Δ ) / (2a) .
- Keď Δ = 0, existuje jeden koreň x 1 = x 2 = -b / (2a) .
- Keď Δ <0, neexistujú žiadne skutočné korene, sú 2 komplexné korene:
x 1 = (- b + i√ -Δ ) / (2a) a x 2 = (- bi√ -Δ ) / (2a) .
Problém č. 1
3 x 2 +5 x +2 = 0
Riešenie:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problém č. 2
3 x 2 -6 x +3 = 0
Riešenie:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problém č. 3
x 2 + 2 x +5 = 0
Riešenie:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Skutočné riešenia neexistujú. Hodnoty sú komplexné čísla:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Graf kvadratickej funkcie
Kvadratická funkcia je polynomiálna funkcia druhého rádu:
f ( x ) = sekera 2 + bx + c
Riešením kvadratickej rovnice sú korene kvadratickej funkcie, ktoré sú priesečníkmi grafu kvadratickej funkcie s osou x, keď
f ( x ) = 0
Ak existujú 2 priesečníky grafu s osou x, existujú dve riešenia kvadratickej rovnice.
Ak je v grafe 1 priesečník grafu s osou x, existuje kvadratická rovnica v 1 riešení.
Keď neexistujú priesečníky grafu s osou x, nedostaneme reálne riešenia (alebo 2 komplexné riešenia).