Pravidlá logaritmu
Základňa b logaritmus radu je exponent , že musíme zvýšiť základňu s cieľom získať telefónne číslo.
- Definícia logaritmu
- Pravidlá logaritmu
- Problémy s logaritmom
- Komplexný logaritmus
- Graf záznamu (x)
- Logaritmická tabuľka
- Logaritmická kalkulačka
Definícia logaritmu
Keď je b zvýšené na mocninu y rovná sa x:
b y = x
Potom sa základný b logaritmus x rovná y:
log b ( x ) = y
Napríklad keď:
2 4 = 16
Potom
log 2 (16) = 4
Logaritmus ako inverzná funkcia exponenciálnej funkcie
Logaritmická funkcia,
y = log b ( x )
je inverzná funkcia exponenciálnej funkcie,
x = b y
Takže ak vypočítame exponenciálnu funkciu logaritmu x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Alebo ak vypočítame logaritmus exponenciálnej funkcie x,
f -1 ( f ( x )) = log b ( b x ) = x
Prirodzený logaritmus (ln)
Prirodzený logaritmus je logaritmus k základu e:
ln ( x ) = prihlásiť e ( x )
Keď e konštanta je číslo:
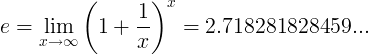
alebo
![]()
Pozri: Prirodzený logaritmus
Výpočet inverzného logaritmu
Inverzný logaritmus (alebo antilogaritmus) sa počíta tak, že sa báza b zvýši na logaritmus y:
x = log -1 ( y ) = b y
Logaritmická funkcia
Logaritmická funkcia má základnú formu:
f ( x ) = log b ( x )
Pravidlá logaritmu
| Názov pravidla | Pravidlo |
|---|---|
Pravidlo logaritmického produktu |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Pravidlo kvocientu logaritmu |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Logaritmické pravidlo sily |
log b ( x y ) = y ∙ log b ( x ) |
Logaritmické pravidlo prechodu na základňu |
log b ( c ) = 1 / log c ( b ) |
Pravidlo základnej zmeny logaritmu |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivácia logaritmu |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integrál logaritmu |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritmus záporného čísla |
log b ( x ) nie je definované, keď x ≤ 0 |
Logaritmus 0 |
log b (0) nie je definovaný |
Logaritmus 1 |
log b (1) = 0 |
Logaritmus základne |
log b ( b ) = 1 |
Logaritmus nekonečna |
lim log b ( x ) = ∞, keď x → ∞ |
Pozri: Pravidlá logaritmu
Pravidlo logaritmického produktu
Logaritmus násobenia x a y je súčtom logaritmu x a logaritmu y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Napríklad:
denník 10 (3 ∙ 7) = denník 10 (3) + denník 10 (7)
Pravidlo kvocientu logaritmu
Logaritmus rozdelenia x a y je rozdiel logaritmu x a logaritmu y.
log b ( x / y ) = log b ( x ) - log b ( y )
Napríklad:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmické pravidlo sily
Logaritmus x zvýšený na mocninu y je y-násobok logaritmu x.
log b ( x y ) = y ∙ log b ( x )
Napríklad:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Logaritmické pravidlo prechodu na základňu
Základný b logaritmus c je 1 vydelený základným c logaritmom b.
log b ( c ) = 1 / log c ( b )
Napríklad:
denník 2 (8) = 1 / denník 8 (2)
Pravidlo základnej zmeny logaritmu
Základný b logaritmus x je základný c logaritmus x vydelený základným c logaritmom b.
log b ( x ) = log c ( x ) / log c ( b )
Napríklad pre výpočet log 2 (8) v kalkulačke musíme zmeniť základ na 10:
denník 2 (8) = denník 10 (8) / denník 10 (2)
Pozri: pravidlo zmeny základu protokolu
Logaritmus záporného čísla
Základný b skutočný logaritmus x, keď x <= 0 je nedefinované, keď x je záporné alebo rovné nule:
log b ( x ) nie je definované, keď x ≤ 0
Pozri: protokol záporného čísla
Logaritmus 0
Nulový základný b logaritmus je nedefinovaný:
log b (0) nie je definovaný
Limit základného b logaritmu x, keď sa x blíži k nule, je mínus nekonečno:
![]()
Pozri: log nuly
Logaritmus 1
Základný b logaritmus jednej je nula:
log b (1) = 0
Napríklad základný dva logaritmy jedného sú nula:
log 2 (1) = 0
Pozri: denník jedného
Logaritmus nekonečna
Limita základného b logaritmu x, keď sa x blíži k nekonečnu, sa rovná nekonečnu:
lim log b ( x ) = ∞, keď x → ∞
Pozri: log nekonečna
Logaritmus základne
Základný b logaritmus b je jeden:
log b ( b ) = 1
Napríklad základný dva logaritmy dvoch sú jeden:
log 2 (2) = 1
Logaritmická derivácia
Kedy
f ( x ) = log b ( x )
Potom derivácia f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Pozri: logaritmická derivácia
Logaritmus integrálny
Integrál logaritmu x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Napríklad:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Logaritmická aproximácia
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Komplexný logaritmus
Pre komplexné číslo z:
z = re iθ = x + iy
Komplexný logaritmus bude (n = ... - 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arktán ( y / x ))
Problémy a odpovede na logaritmus
Problém č. 1
Nájdite x pre
log 2 ( x ) + log 2 ( x -3) = 2
Riešenie:
Použitie pravidla produktu:
log 2 ( x ∙ ( x -3)) = 2
Zmena formy logaritmu podľa definície logaritmu:
x ∙ ( x -3) = 2 2
Alebo
x 2 -3 x -4 = 0
Riešenie kvadratickej rovnice:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4,1
Pretože logaritmus nie je definovaný pre záporné čísla, odpoveď znie:
x = 4
Problém č. 2
Nájdite x pre
log 3 ( x +2) - log 3 ( x ) = 2
Riešenie:
Použitie pravidla kvocientu:
log 3 (( x +2) / x ) = 2
Zmena formy logaritmu podľa definície logaritmu:
( x +2) / x = 3 2
Alebo
x +2 = 9 x
Alebo
8 x = 2
Alebo
x = 0,25
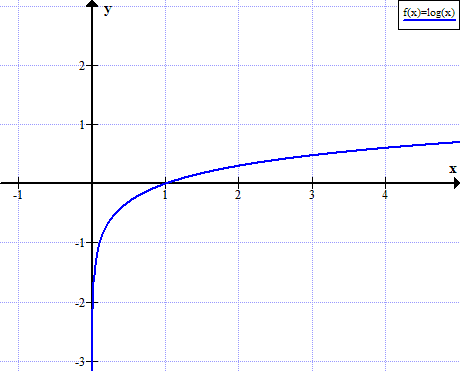
Graf záznamu (x)
log (x) nie je definovaný pre skutočné kladné hodnoty x:
Tabuľka logaritmov
| x | prihlásiť 10 x | prihlásiť 2 x | prihlásiť e x |
|---|---|---|---|
| 0 | nedefinované | nedefinované | nedefinované |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6,643856 | -4,605170 |
| 0,1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,4777121 | 1,584963 | 1,098612 |
| 4 | 0,602060 | 2 | 1,386294 |
| 5 | 0,698970 | 2,321928 | 1,609438 |
| 6 | 0,778151 | 2,584963 | 1,791759 |
| 7 | 0,845098 | 2,807355 | 1,945910 |
| 8 | 0,903090 | 3 | 2,079442 |
| 9 | 0,954243 | 3,169925 | 2,197225 |
| 10 | 1 | 3,321928 | 2,302585 |
| 20 | 1,301030 | 4,321928 | 2,995732 |
| 30 | 1,477121 | 4,906891 | 3,401197 |
| 40 | 1,602060 | 5,321928 | 3,688879 |
| 50 | 1,698970 | 5,643856 | 3,912023 |
| 60 | 1,778151 | 5,906991 | 4,094345 |
| 70 | 1,845098 | 6,299283 | 4,248495 |
| 80 | 1,903090 | 6,321928 | 4,382027 |
| 90 | 1,954243 | 6,49 1853 | 4,499810 |
| 100 | 2 | 6,643856 | 4,605170 |
| 200 | 2,301030 | 7,643856 | 5,198317 |
| 300 | 2,477121 | 8.228819 | 5,703782 |
| 400 | 2,602060 | 8,643856 | 5,991465 |
| 500 | 2,698970 | 8,965784 | 6,214608 |
| 600 | 2,778151 | 9,28819 | 6,396930 |
| 700 | 2,845098 | 9,451211 | 6,551080 |
| 800 | 2,903090 | 9,643856 | 6,684612 |
| 900 | 2,954243 | 9,813781 | 6,802395 |
| 1 000 | 3 | 9,965784 | 6,907755 |
| 10 000 | 4 | 13,287712 | 9,210340 |
Pozri tiež
- Pravidlá logaritmu
- Logaritmická zmena základne
- Logaritmus nuly
- Logaritmus jedného
- Logaritmus nekonečna
- Logaritmus záporného čísla
- Logaritmická kalkulačka
- Logaritmický graf
- Logaritmická tabuľka
- Prirodzená logaritmická kalkulačka
- Prirodzený logaritmus - ln x
- e konštantná
- Decibel (dB)