Konvolúcia
Konvolúcia je korelačná funkcia f (τ) s obrátenou funkciou g (t-τ).
Konvolučný operátor je symbol hviezdičky * .
- Nepretržitá konvolúcia
- Diskrétna konvolúcia
- 2D diskrétna konvolúcia
- Filtrovať implementáciu pomocou konvolúcie
- Konvolučná veta
Nepretržitá konvolúcia
Konvolúcia f (t) a g (t) sa rovná integrálu f (τ) krát f (t-τ):
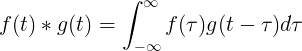
Diskrétna konvolúcia
Konvolúcia 2 samostatných funkcií je definovaná ako:
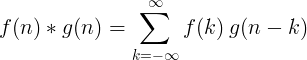
2D diskrétna konvolúcia
Na spracovanie obrazu sa zvyčajne používa dvojrozmerná diskrétna konvolúcia.
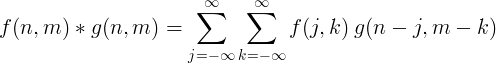
Filtrovať implementáciu pomocou konvolúcie
Diskrétny vstupný signál x (n) môžeme filtrovať konvolúciou s impulznou odozvou h (n), aby sme dostali výstupný signál y (n).
y ( n ) = x ( n ) * h ( n )
Konvolučná veta
Fourierova transformácia násobenia 2 funkcií sa rovná konvolúcii Fourierových transformácií každej funkcie:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Fourierova transformácia konvolúcie 2 funkcií sa rovná násobeniu Fourierovej transformácie každej funkcie:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Konvolučná veta pre spojitú Fourierovu transformáciu
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konvolučná veta pre diskrétnu Fourierovu transformáciu
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Konvolučná veta pre Laplaceovu transformáciu
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Pozri tiež
CALCULUS
- Obmedziť
- Derivát
- Integrálne
- Séria
- Laplaceova transformácia
- Konvolúcia
- Početné symboly
RÝCHLE TABUĽKY