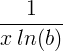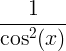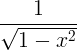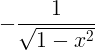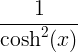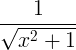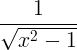Odvodené pravidlá
Odvodené pravidlá a zákony. Tabuľka derivácií funkcií.
Derivátová definícia
Deriváciou funkcie je pomer rozdielu funkčnej hodnoty f (x) v bodoch x + Δx a x s Δx, keď je Δx nekonečne malý. Deriváciou je funkčný sklon alebo sklon dotyčnice v bode x.
![]()
Druhá derivácia
Druhá derivácia je daná:
![]()
Alebo jednoducho odvodte prvú deriváciu:
![]()
N-tý derivát
N th derivát sa vypočíta odvodenie f (x) n-krát.
K n th derivát sa rovná derivát (n-1) derivát:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Príklad:
Nájdite štvrtú deriváciu
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '= [10 x 4 ]' '= = [40 x 3 ]' '= [120 x 2 ]' = 240 x
Derivát na grafe funkcie
Derivátom funkcie je slop tangenciálnej čiary.
Odvodené pravidlá
| Pravidlo odvodenej sumy | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Pravidlo odvodeného produktu | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Derivačné pravidlo kvocientu | 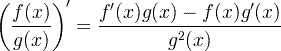 |
| Odvodené reťazcové pravidlo | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Pravidlo odvodenej sumy
Keď a a b sú konštanty.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Príklad:
Nájdite derivát:
3 x 2 + 4 x.
Podľa pravidla súčtu:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Pravidlo odvodeného produktu
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Derivačné pravidlo kvocientu
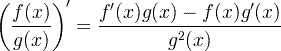
Odvodené reťazcové pravidlo
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Toto pravidlo možno lepšie pochopiť pomocou Lagrangeovej notácie:
![]()
Lineárna aproximácia funkcie
Pre malé Δx môžeme získať aproximáciu f (x 0 + Δx), keď poznáme f (x 0 ) a f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Tabuľka derivácií funkcií
| Názov funkcie | Funkcia | Derivát |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Neustále | konšt |
0 |
| Lineárne | x |
1 |
| Moc | x a |
sekera a- 1 |
| Exponenciálny | e x |
e x |
| Exponenciálny | a x |
a x ln a |
| Prirodzený logaritmus | ln ( x ) |
|
| Logaritmus | denník b ( x ) |
|
| Sínus | hriech x |
cos x |
| Kosínus | cos x |
-hrebe x |
| Tečna | opáliť x |
|
| Arcsine | arcsin x |
|
| Arkkozín | arccos x |
|
| Arkustangens | arctan x |
|
| Hyperbolický sínus | sinh x |
keš x |
| Hyperbolický kosínus | keš x |
sinh x |
| Hyperbolická tangenta | tanh x |
|
| Inverzný hyperbolický sínus | sinh -1 x |
|
| Inverzný hyperbolický kosínus | keš -1 x |
|
| Inverzná hyperbolická tangens | tanh -1 x |
|
Derivačné príklady
Príklad č
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Príklad č
f ( x ) = hriech (3 x 2 )
Pri uplatňovaní reťazového pravidla:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Druhý derivačný test
Keď je prvá derivácia funkcie v bode x 0 nulová .
f '( x 0 ) = 0
Potom druhá derivácia v bode x 0 , f '(x 0 ), môže označovať typ tohto bodu:
| f "( x 0 )/ 0 |
miestne minimum |
| f "( x 0 ) <0 |
miestne maximum |
| f "( x 0 ) = 0 |
neurčené |
Pozri tiež
CALCULUS
- Obmedziť
- Derivát
- Integrálne
- Séria
- Laplaceova transformácia
- Konvolúcia
- Početné symboly
RÝCHLE TABUĽKY