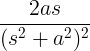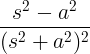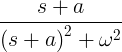Laplaceova transformácia

Laplaceova transformácia prevádza funkciu časovej domény na funkciu s-doména integráciou z nuly do nekonečna

funkcie časovej domény, vynásobené e ^-st .

Laplaceova transformácia sa používa na rýchle nájdenie riešení diferenciálnych rovníc a integrálov.

Odvodenie v časovej doméne sa transformuje na násobenie s v s-doméne.

Integrácia v časovej doméne sa transformuje na delenie s v s-doméne.

Laplaceova transformačná funkcia

Laplaceova transformácia je definovaná operátorom L {}:

$F (s) = \ mathcal {L} \ dolava \ {f (t) \ doprava \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Inverznú Laplaceovu transformáciu je možné vypočítať priamo.

Zvyčajne je inverzná transformácia daná z tabuľky transformácií.

Názov funkcie	Funkcia časovej domény	Laplaceova transformácia
Názov funkcie	f ( t )	F ( s ) = L { f ( t )}
Neustále	1	$\ frac {1} {s}$
Lineárne	t	$\ frac {1} {s ^ 2}$
Moc	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Moc	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponent	e ^o	$\ frac {1} {sa}$
Sínus	hrešiť o	$\ frac {a} {s ^ 2 + a ^ 2}$
Kosínus	pretože o	$\ frac {s} {s ^ 2 + a ^ 2}$
Hyperbolický sínus	hrešiť na	$\ frac {a} {s ^ 2-a ^ 2}$
Hyperbolický kosínus	hovienka na	$\ frac {s} {s ^ 2-a ^ 2}$
Rastúci sínus	t hriech pri	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Rastúci kosínus	t cos pri	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Rozpadajúci sa sínus	e ^-at sin ωt	$\ frac {\ omega} {\ doľava (s + a \ doprava) ^ 2 + \ omega ^ 2}$
Rozkladajúci sa kosínus	e ^-at cos ωt	$\ frac {s + a} {\ doľava (s + a \ doprava) ^ 2 + \ omega ^ 2}$
Delta funkcia	δ ( t )	1
Oneskorená delta	δ ( ta )	e- ^ako

Názov nehnuteľnosti	Funkcia časovej domény	Laplaceova transformácia	Komentovať
	f ( t )	F ( s )
Lineárnosť	af ( t ) + bg ( t )	aF ( y ) + bG ( y )	a , b sú konštantné
Zmena mierky	f ( zavináč )	$\ frac {1} {a} F \ doľava (\ frac {s} {a} \ doprava)$	a / 0
Posun	e ^-at f ( t )	F ( s + a )
Oneskorenie	f ( ta )	e ^{- ako} F ( s )
Odvodenie	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-tá derivácia	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Moc	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integrácia	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F$
Obojstranný	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Konvolúcia	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* je operátor konvolúcie
Periodická funkcia	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$