Štandardná odchýlka

V pravdepodobnosti a štatistike je štandardnou odchýlkou náhodnej premennej priemerná vzdialenosť náhodnej premennej od strednej hodnoty.

Predstavuje to, ako je náhodná premenná distribuovaná v blízkosti strednej hodnoty. Malá štandardná odchýlka naznačuje, že náhodná premenná je distribuovaná v blízkosti strednej hodnoty. Veľká štandardná odchýlka naznačuje, že náhodná premenná je distribuovaná ďaleko od strednej hodnoty.

Vzorec na definíciu štandardnej odchýlky

Štandardná odchýlka je druhá odmocnina rozptylu náhodnej premennej X so strednou hodnotou μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Z definície štandardnej odchýlky môžeme dostať

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Štandardná odchýlka spojitej náhodnej premennej

Pre spojitú náhodnú veličinu so strednou hodnotou μ a funkciou hustoty pravdepodobnosti f (x):

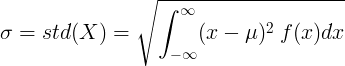
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

alebo

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Štandardná odchýlka diskrétnej náhodnej premennej

Pre diskrétnu náhodnú premennú X so strednou hodnotou μ a funkciou pravdepodobnosti hmotnosti P (x):

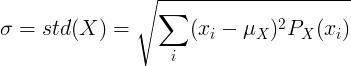
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

alebo

\ sigma = std (X) = \ sqrt {\ doľava [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ doprava] - \ mu ^ 2}

 

Rozdelenie pravdepodobnosti ►

 

Pozri tiež

PRAVDEPODOBNOSŤ A ŠTATISTIKA
RÝCHLE TABUĽKY