Kvadratna enačba
Kvadratna enačba je polinom drugega reda s 3 koeficienti - a , b , c .
Kvadratna enačba je podana z:
sekira 2 + bx + c = 0
Rešitev kvadratne enačbe je podana z dvema številkama x 1 in x 2 .
Kvadratno enačbo lahko spremenimo v obliko:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratna formula
Rešitev kvadratne enačbe poda kvadratna formula:
![]()
Izraz znotraj kvadratnega korena se imenuje diskriminanten in je označen z Δ:
Δ = b 2 - 4 ac
Kvadratna formula z diskriminatornim zapisom:
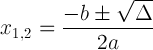
Ta izraz je pomemben, ker nam lahko pove o rešitvi:
- Ko je Δ/ 0, obstajata 2 realni korenini x 1 = (- b + √ Δ ) / (2a) in x 2 = (- b-√ Δ ) / (2a) .
- Ko je Δ = 0, obstaja en koren x 1 = x 2 = -b / (2a) .
- Če obstajajo Δ <0 ni prave korenine, obstajajo 2 zapletene korenine:
x 1 = (- b + i√ -Δ ) / (2a) in x 2 = (- bi√ -Δ ) / (2a) .
Problem 1
3 x 2 +5 x +2 = 0
rešitev:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem 2
3 x 2 -6 x +3 = 0
rešitev:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem 3
x 2 +2 x +5 = 0
rešitev:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Pravih rešitev ni. Vrednosti so kompleksna števila:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratni graf funkcij
Kvadratna funkcija je polinomska funkcija drugega reda:
f ( x ) = os 2 + bx + c
Rešitve kvadratne enačbe so korenine kvadratne funkcije, ki so presečišča grafa kvadratne funkcije z osjo x, ko
f ( x ) = 0
Ko sta dve presečišči grafa z osjo x, obstajata dve rešitvi kvadratne enačbe.
Ko je 1 presečišče grafa z osjo x, obstaja 1 rešitev kvadratne enačbe.
Ko ni presečišč grafa z osjo x, ne dobimo resničnih rešitev (ali 2 kompleksni rešitvi).