Naravni logaritem - ln (x)

Naravni logaritem je logaritem za osnovo e števila.

Opredelitev naravnega logaritma

Kdaj

e y = x

Potem je osnovni e logaritem x

ln ( x ) = log e ( x ) = y

 

E konstanta ali številka Eulerjev je:

e ≈ 2,71828183

Ln kot inverzna funkcija eksponentne funkcije

Funkcija naravnega logaritma ln (x) je inverzna funkcija eksponentne funkcije e x .

Za x/ 0,

f ( f -1 ( x )) = e ln ( x ) = x

Ali

f -1 ( f ( x )) = ln ( e x ) = x

Pravila in lastnosti naravnega logaritma

Ime pravila Pravilo Primer
Pravilo izdelka

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
Pravilo količnika

ln ( x / y ) = ln ( x ) - ln ( y )

ln (3 / 7) = ln (3) - ln (7)
Pravilo moči

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
V izpeljanki
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
V celoti
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
ln negativnega števila
 ln ( x ) ni opredeljen, kadar je x ≤ 0  
Nič
 ln (0) ni opredeljeno  
 
V enem
 ln (1) = 0  
V neskončnosti
 lim ln ( x ) = ∞, ko je x → ∞  
Eulerjeva identiteta ln (-1) = i π  

 

Pravilo logaritemskega izdelka

Logaritem množenja x in y je vsota logaritma x in logaritma y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Na primer:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Pravilo količnika logaritma

Logaritem delitve x in y je razlika logaritma x in logaritma y.

log b ( x / y ) = log b ( x ) - log b ( y )

Na primer:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Pravilo moči logaritma

Logaritem x, dvignjen na stopnjo y, je y pomnožen z logaritmom x.

log b ( x y ) = y ∙ log b ( x )

Na primer:

log 10 (2 8 ) = 8 ∙ log 10 (2)

Izpeljanka naravnega logaritma

Izpeljanka funkcije naravnega logaritma je vzajemna funkcija.

Kdaj

f ( x ) = ln ( x )

Izvedek f (x) je:

f ' ( x ) = 1 / x

Integral naravnega logaritma

Integral funkcije naravnega logaritma je podan z:

Kdaj

f ( x ) = ln ( x )

Integral f (x) je:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln od 0

Naravni logaritem nič ni opredeljen:

ln (0) ni opredeljeno

Meja blizu 0 naravnega logaritma x, ko se x približa ničli, je minus neskončnost:

Ln od 1

Naravni logaritem ena je nič:

ln (1) = 0

Ln neskončnosti

Meja naravnega logaritma neskončnosti, ko se x približuje neskončnosti, je enaka neskončnosti:

lim ln ( x ) = ∞, ko je x → ∞

Kompleksni logaritem

Za kompleksno število z:

z = re iθ = x + iy

Kompleksni logaritem bo (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

Graf ln (x)

ln (x) ni definiran za realne pozitivne vrednosti x:

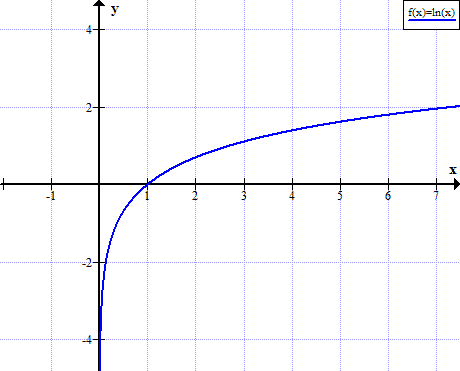
Tabela naravnih logaritmov

x ln x
0 nedoločeno
0 + - ∞
0,0001 -9,210340
0,001 -6,907755
0,01 -4.605170
0,1 -2.302585
1 0
2 0,693147
e ≈ 2,7183 1
3 1.098612
4 1.386294
5 1.609438
6 1,791759
7 1.945910
8 2.079442
9 2.197225
10 2,302585
20 2.995732
30 3.401197
40 3,688879
50 3,912023
60 4.094345
70 4.248495
80 4.382027
90 4,499810
100 4,605170
200 5.298317
300 5,703782
400 5.991465
500 6.214608
600 6,396930
700 6,551080
800 6,684612
900 6.802395
1000 6.907755
10000 9.210340

 

Pravila logaritma ►

 

Poglej tudi

ALGEBRA
HITRE MIZE