Конволуција

Конволација је корелациона функција ф (τ) са обрнутом функцијом г (т-τ).

Оператор конволуције је симбол звездице * .

Конволација ф (т) и г (т) једнака је интегралу ф (τ) пута ф (т-τ):

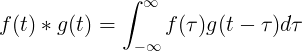
$ф (т) * г (т) = \ инт _ {- \ инфти} ^ {\ инфти} ф (\ тау) г (т- \ тау) д \ тау$

Конволација 2 дискретне функције дефинисана је као:

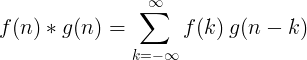
$ф (н) * г (н) = \ сум_ {к = - \ инфти} ^ {\ инфти} ф (к) \: г (нк)$

Дводимензионална дискретна конволуција се обично користи за обраду слике.

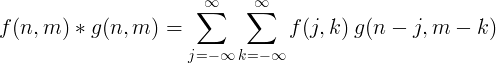
$ф (н, м) * г (н, м) = \ сум_ {ј = - \ инфти} ^ {\ инфти} \ сум_ {к = - \ инфти} ^ {\ инфти} ф (ј, к) \: г (њ, мк)$

Дискретни улазни сигнал к (н) можемо филтрирати конволуцијом са импулсним одзивом х (н) да бисмо добили излазни сигнал и (н).

и ( н ) = к ( н ) * х ( н )

Фуријеова трансформација множења 2 функције једнака је конволуцији Фуријеових трансформација сваке функције:

ℱ { ф ⋅ г } = ℱ { ф } * ℱ { г }

Фуријеова трансформација конволуције од 2 функције једнака је множењу Фуријеових трансформација сваке функције:

ℱ { ф * г } = ℱ { ф } ℱ г { г }

ℱ { ф ( т ) ⋅ г ( т )} = ℱ { ф ( т )} * ℱ { г ( т )} = Ф ( ω ) * Г ( ω )

ℱ { ф ( т ) * г ( т )} = ℱ { ф ( т )} ⋅ ℱ { г ( т )} = Ф ( ω ) ⋅ Г ( ω )

ℱ { ф ( н ) ⋅ г ( н )} = ℱ { ф ( н )} * ℱ { г ( н )} = Ф ( к ) * Г ( к )

ℱ { ф ( н ) * г ( н )} = ℱ { ф ( н )} ⋅ ℱ { г ( н )} = Ф ( к ) ⋅ Г ( к )

ℒ { ф ( т ) * г ( т )} = ℒ { ф ( т )} ⋅ ℒ { г ( т )} = Ф ( с ) ⋅ Г ( с )

Такође видети