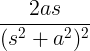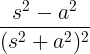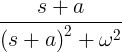Лаплацеова трансформација

Лаплацеова трансформација претвара функцију временског домена у функцију с-домена интеграцијом од нуле до бесконачности

функције временског домена, помножено са е ^-ст .

Лапласова трансформација се користи за брзо проналажење решења за диференцијалне једначине и интеграле.

Извођење у временском домену трансформише се у множење с у с-домену.

Интеграција у временском домену трансформише се у дељење с у с-домену.

Лапласова функција трансформације

Лапласова трансформација је дефинисана оператором Л {}:

$Ф (с) = \ матхцал {Л} \ лево \ {ф (т) \ десно \} = \ инт_ {0} ^ {\ инфти} е ^ {- ст} ф (т) дт$

Инверзна Лапласова трансформација може се израчунати директно.

Обично је инверзна трансформација дата из табеле трансформација.

Назив функције	Функција временског домена	Лапласова трансформација
Назив функције	ф ( т )	Ф ( с ) = Л { ф ( т )}
Стално	1	$\ фрац {1} {с}$
Линеарно	т	$\ фрац {1} {с ^ 2}$
Снага	т ^н	$\ фрац {н!} {с ^ {н + 1}}$
Снага	т ^а	Γ ( + 1) ⋅ ова^{- (}^{+ 1)}
Експонент	е ^ат	$\ фрац {1} {са}$
Сине	грешити на	$\ фрац {а} {с ^ 2 + а ^ 2}$
Цосине	цос ат	$\ фрац {с} {с ^ 2 + а ^ 2}$
Хиперболични синус	синх ат	$\ фрац {а} {с ^ 2-а ^ 2}$
Хиперболични косинус	цосх ат	$\ фрац {с} {с ^ 2-а ^ 2}$
Узгајање синуса	т грешити на	$\ фрац {2ас} {(с ^ 2 + а ^ 2) ^ 2}$
Расте косинус	т цос ат	$\ фрац {с ^ 2-а ^ 2} {(с ^ 2 + а ^ 2) ^ 2}$
Пропадајући синус	Е ^-На грех ωт	$\ фрац {\ омега} {\ лево (с + а \ десно) ^ 2 + \ омега ^ 2}$
Пропадајући косинус	Е ^-На јер ωт	$\ фрац {с + а} {\ лево (с + а \ десно) ^ 2 + \ омега ^ 2}$
Делта функција	δ ( т )	1
Одложена делта	δ ( та )	е ^-ас

Назив својства	Функција временског домена	Лапласова трансформација	Коментар
	ф ( т )	Ф ( с )
Линеарност	аф ( т ) + бг ( т )	аФ ( с ) + бГ ( с )	а , б су константне
Промена скале	ф ( ат )	$\ фрац {1} {а} Ф \ лево (\ фрац {с} {а} \ десно)$	а / 0
Смена	е ^-ат ф ( т )	Ф ( с + а )
Кашњење	ф ( та )	е ^{- као} Ф ( с )
Извођење	$\ фрац {дф (т)} {дт}$	сФ ( с ) - ф (0)
Н-ти извод	$\ фрац {д ^ нф (т)} {дт ^ н}$	с ^н ф ( с ) - с ^{н -1}ф (0) - с ^{н -2}ф '(0) -...- ф ^{( н -1)} (0)
Снага	т ^н ф ( т )	$(-1) ^ н \ фрац {д ^ нФ (с)} {дс ^ н}$
Интеграција	$\ инт_ {0} ^ {т} ф (к) дк$	$\ фрац {1} {с} Ф (с)$
Узајамно	$\ фрац {1} {т} ф (т)$	$\ инт_ {с} ^ {\ инфти} Ф (к) дк$
Конволуција	ф ( т ) * г ( т )	Ф ( с ) ⋅ Г ( с )	* је оператор савијања
Периодична функција	ф ( т ) = ф ( т + Т )	$\ фрац {1} {1-е ^ {- сТ}} \ инт_ {0} ^ {Т} е ^ {- ск} ф (к) дк$