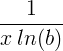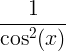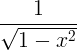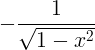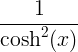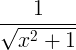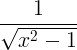Изведена правила
Изведена правила и закони. Табела деривата функција.
Дефиниција деривата
Извод функције је однос разлике вредности функције ф (к) у тачкама к + Δк и к са Δк, када је Δк бесконачно мали. Извод је нагиб функције или нагиб тангенте у тачки к.
![]()
Друга изведеница
Други дериват је дат:
![]()
Или једноставно изведите први дериват:
![]()
Н-ти дериват
Н тх дериват израчунава извођења ф (к) н пута.
У н тх деривативе једнака дериват (н-1) дериват:
ф ( н ) ( к ) = [ ф ( н -1) ( к )] '
Пример:
Нађи четврту изведеницу од
ф ( к ) = 2 к 5
ф (4) ( к ) = [2 к 5 ] '' '' = [10 к 4 ] '' '= [40 к 3 ]' '= [120 к 2 ]' = 240 к
Дериват на графикону функције
Извод функције је нагиб тангенцијалне линије.
Изведена правила
| Правило дериватне суме | ( аф ( к ) + бг ( к )) '= аф' ( к ) + бг ' ( к ) |
| Правило изведеног производа | ( ф ( к ) ∙ г ( к )) '= ф' ( к ) г ( к ) + ф ( к ) г ' ( к ) |
| Изведено количничко правило | 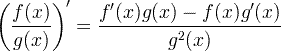 |
| Правило изведеног ланца | ф ( г ( к )) '= ф' ( г ( к )) ∙ г ' ( к ) |
Правило дериватне суме
Када су а и б константе.
( аф ( к ) + бг ( к )) '= аф' ( к ) + бг ' ( к )
Пример:
Пронађи изведеницу од:
3 к 2 + 4 к.
Према правилу збира:
а = 3, б = 4
ф ( к ) = к 2 , г ( к ) = к
ф ' ( к ) = 2 к , г' ( к ) = 1
(3 к 2 + 4 к ) '= 3⋅2 к + 4⋅1 = 6 к + 4
Правило изведеног производа
( ф ( к ) ∙ г ( к )) '= ф' ( к ) г ( к ) + ф ( к ) г ' ( к )
Изведено количничко правило
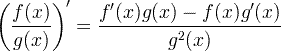
Правило изведеног ланца
ф ( г ( к )) '= ф' ( г ( к )) ∙ г ' ( к )
Ово правило се може боље разумети помоћу Лагрангеове нотације:
![]()
Функција линеарне апроксимације
За мали Δк, можемо добити апроксимацију ф (к 0 + Δк), када знамо ф (к 0 ) и ф '(к 0 ):
ф ( к 0 + Δ к ) ≈ ф ( к 0 ) + ф '( к 0 ) ⋅Δ к
Табела деривата функција
| Назив функције | Функција | Деривативни |
|---|---|---|
| ф ( к ) |
ф '( к ) | |
| Стално | цонст |
0 |
| Линеарно | к |
1 |
| Снага | к а |
секира а- 1 |
| Експоненцијално | е к |
е к |
| Експоненцијално | а к |
а к лн а |
| Природни логаритам | лн ( к ) |
|
| Логаритам | лог б ( к ) |
|
| Сине | син к |
цос к |
| Цосине | цос к |
-син к |
| Тангента | тан к |
|
| Арцсине | арцсин к |
|
| Арццосине | арццос к |
|
| Арцтангент | арцтан к |
|
| Хиперболични синус | синх к |
цосх к |
| Хиперболични косинус | цосх к |
синх к |
| Хиперболична тангента | танх к |
|
| Инверзни хиперболични синус | синх -1 х |
|
| Инверзни хиперболични косинус | цосх -1 к |
|
| Инверзна хиперболична тангента | танх -1 к |
|
Изведени примери
Пример # 1
ф ( к ) = к 3 +5 к 2 + к +8
ф ' ( к ) = 3 к 2 + 2⋅5 к + 1 + 0 = 3 к 2 +10 к +1
Пример # 2
ф ( к ) = грех (3 к 2 )
Када примените правило ланца:
ф ' ( к ) = цос (3 к 2 ) ⋅ [3 к 2 ]' = цос (3 к 2 ) ⋅ 6 к
Други тест деривата
Када је први извод функције нула у тачки к 0 .
ф '( к 0 ) = 0
Тада други извод у тачки к 0 , ф '' (к 0 ), може означавати тип те тачке:
| ф '' ( к 0 )/ 0 |
локални минимум |
| ф '' ( к 0 ) <0 |
локални максимум |
| ф '' ( к 0 ) = 0 |
неодређено |
Такође видети
КАЛКУЛ
- Лимит
- Деривативни
- Интеграл
- Сериес
- Лапласова трансформација
- Конволуција
- Симболи рачуна
БРЗЕ ТАБЛИЦЕ