Veck
Konvolution är korrelationsfunktionen för f (τ) med den omvända funktionen g (t-τ).
Konvolutionsoperatören är asterisk-symbolen * .
- Kontinuerlig faltning
- Diskret faltning
- 2D diskret fällning
- Filtrera implementering med faltning
- Sammansättningssats
Kontinuerlig faltning
Konvolutionen av f (t) och g (t) är lika med integralen av f (τ) gånger f (t-τ):
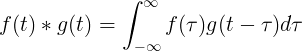
Diskret faltning
Konvolution av två separata funktioner definieras som:
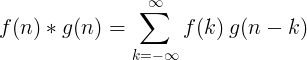
2D diskret fällning
Tvådimensionell diskret konvolution används vanligtvis för bildbehandling.
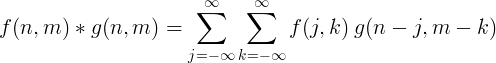
Filtrera implementering med faltning
Vi kan filtrera den diskreta insignalen x (n) genom faltning med impulsresponsen h (n) för att få utsignalen y (n).
y ( n ) = x ( n ) * h ( n )
Sammansättningssats
Fouriertransformationen av en multiplikation av två funktioner är lika med fällningen av Fouriertransformerna för varje funktion:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Fouriertransformationen av en faltning av två funktioner är lika med multipliceringen av Fourier-transformationerna för varje funktion:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Sammansättningssats för kontinuerlig Fourier-transformation
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Sammansättningssats för diskret Fourier-transformation
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Sammansättningssats för Laplace-transform
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )