Arccos (x) -funktion
Arccos (x), cos -1 (x), invers cosinusfunktion .
Arccos definition
Arccosine av x definieras som den inversa cosinusfunktionen av x när -1≤x≤1.
När cosinus av y är lika med x:
cos y = x
Då är arkkosinen av x lika med den inversa cosinusfunktionen av x, som är lika med y:
arccos x = cos -1 x = y
(Här betyder cos -1 x det inversa cosinus och betyder inte cosinus till kraften -1).
Exempel
arccos 1 = cos -1 1 = 0 rad = 0 °
Diagram över arccos
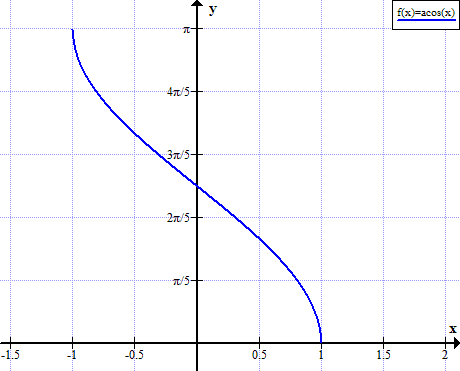
Arccos reglerar
| Regelnamn | Regel |
|---|---|
| Cosinus av arccosine | cos (arccos x ) = x |
| Arccosine of cosinus | arccos (cos x ) = x + 2 k π, när k ∈ℤ ( k är heltal) |
| Arccos av negativa argument | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Kompletterande vinklar | bågar x = π / 2 - bågar x = 90 ° - bågar x |
| Arccos summa | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos skillnad | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos of sin of x | arccos (sin x ) = - x - (2 k +0,5) π |
| Sinus av arccosine | |
| Tangent av arkkosin | 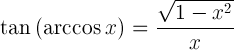 |
| Derivat av arkkosin | 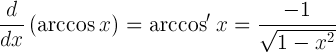 |
| Obestämd integral av arccosine | |
Arccos bord
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ tre / 2 | 5π / 6 | 150 ° |
| -√ två / två | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Se även
- Kosinusfunktion
- Arcsine-funktion
- Arktanfunktion
- Arccos miniräknare
- Radianer till graderomvandlare
- Arccos av 0
- Arccos av 1
- Arccos av 2
- Arccos av 3
- Arccos of cos
- Syndens bågar
- Arccos-derivat
- Arccos-diagram
- För arccos
- Synd av arccos
- Brun av arccos