இருபடி சமன்பாடு
இருபடி சமன்பாடு 3 குணகங்களைக் கொண்ட இரண்டாவது வரிசை பல்லுறுப்புக்கோவை - a , b , c .
இருபடி சமன்பாடு வழங்கியது:
கோடாரி 2 + பிஎக்ஸ் + சி = 0
இருபடி சமன்பாட்டிற்கான தீர்வு 2 எண்கள் x 1 மற்றும் x 2 ஆல் வழங்கப்படுகிறது .
இருபடி சமன்பாட்டை நாம் இதன் வடிவத்திற்கு மாற்றலாம்:
( x - x 1 ) ( x - x 2 ) = 0
இருபடி ஃபார்முலா
இருபடி சமன்பாட்டிற்கான தீர்வு இருபடி சூத்திரத்தால் வழங்கப்படுகிறது:
![]()
சதுர மூலத்தின் வெளிப்பாடு பாகுபாடு என்று அழைக்கப்படுகிறது மற்றும் இது by ஆல் குறிக்கப்படுகிறது
= ப 2 - 4 ஏசி
பாரபட்சமான குறியீட்டைக் கொண்ட இருபடி சூத்திரம்:
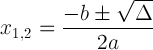
இந்த வெளிப்பாடு முக்கியமானது, ஏனெனில் இது தீர்வைப் பற்றி சொல்ல முடியும்:
- Δ/ 0 போது, 2 உண்மையான வேர்கள் x 1 = (- b + √ Δ ) / (2a) மற்றும் x 2 = (- b- Δ ) / (2a) உள்ளன .
- Δ = 0 போது, ஒரு வேர் x 1 = x 2 = -b / (2a) உள்ளது .
- Δ <0 போது, உண்மையான வேர்கள் இல்லை, 2 சிக்கலான வேர்கள் உள்ளன:
x 1 = (- b + i√ -Δ ) / (2a) மற்றும் x 2 = (- bi√ -Δ ) / (2a) .
சிக்கல் # 1
3 x 2 +5 x +2 = 0
தீர்வு:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
சிக்கல் # 2
3 x 2 -6 x +3 = 0
தீர்வு:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
சிக்கல் # 3
x 2 +2 x +5 = 0
தீர்வு:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
உண்மையான தீர்வுகள் எதுவும் இல்லை. மதிப்புகள் சிக்கலான எண்கள்:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
இருபடி செயல்பாடு வரைபடம்
இருபடி செயல்பாடு இரண்டாவது வரிசை பல்லுறுப்புறுப்பு செயல்பாடு:
f ( x ) = கோடாரி 2 + பிஎக்ஸ் + சி
இருபடி சமன்பாட்டிற்கான தீர்வுகள் இருபடிச் செயல்பாட்டின் வேர்கள், அவை x- அச்சுடன் இருபடி செயல்பாட்டு வரைபடத்தின் குறுக்குவெட்டு புள்ளிகள், எப்போது
f ( x ) = 0
X- அச்சுடன் வரைபடத்தின் 2 குறுக்குவெட்டு புள்ளிகள் இருக்கும்போது, இருபடி சமன்பாட்டிற்கு 2 தீர்வுகள் உள்ளன.
X- அச்சுடன் வரைபடத்தின் 1 குறுக்குவெட்டு புள்ளி இருக்கும்போது, இருபடி சமன்பாட்டிற்கு 1 தீர்வு உள்ளது.
X- அச்சுடன் வரைபடத்தின் குறுக்குவெட்டு புள்ளிகள் இல்லாதபோது, உண்மையான தீர்வுகள் (அல்லது 2 சிக்கலான தீர்வுகள்) கிடைக்காது.