இயற்கை மடக்கை - ln (x)
இயற்கையான மடக்கை என்பது ஒரு எண்ணின் அடிப்படை e க்கான மடக்கை ஆகும்.
- இயற்கை மடக்கை (ln) வரையறை
- இயற்கை மடக்கை (எல்என்) விதிகள் & பண்புகள்
- சிக்கலான மடக்கை
- Ln (x) இன் வரைபடம்
- இயற்கை மடக்கைகள் (ln) அட்டவணை
- இயற்கை மடக்கை கால்குலேட்டர்
இயற்கையான மடக்கை வரையறை
எப்பொழுது
e y = x
X இன் அடிப்படை e மடக்கை
ln ( x ) = பதிவு e ( x ) = y
இ நிலையான அல்லது ஆய்லரின் எண்:
e 2.71828183
அதிவேக செயல்பாட்டின் தலைகீழ் செயல்பாடாக எல்.என்
இயற்கையான மடக்கை செயல்பாடு ln (x) என்பது அதிவேக செயல்பாட்டின் தலைகீழ் செயல்பாடு e x .
X/ 0 க்கு,
f ( f -1 ( x )) = e ln ( x ) = x
அல்லது
f -1 ( f ( x )) = ln ( e x ) = x
இயற்கை மடக்கை விதிகள் மற்றும் பண்புகள்
| விதி பெயர் | விதி | உதாரணமாக |
|---|---|---|
தயாரிப்பு விதி |
ln ( x y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
அளவு விதி |
ln ( x / y ) = ln ( x ) - ln ( y ) |
Ln (3 / 7) இச்சார்புக்கு (3) - Ln (7) |
சக்தி விதி |
ln ( x y ) = y ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
ln வழித்தோன்றல் |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
ln ஒருங்கிணைந்த |
∫ Ln ( எக்ஸ் ) டிஎக்ஸ் = எக்ஸ் ∙ (Ln ( எக்ஸ் ) - 1) + சி | |
எதிர்மறை எண்ணின் ln |
x ≤ 0 போது ln ( x ) வரையறுக்கப்படவில்லை | |
ln பூஜ்ஜியம் |
ln (0) வரையறுக்கப்படவில்லை | |
ஒன்றின் ln |
ln (1) = 0 | |
முடிவிலி ln |
லிம் Ln ( எக்ஸ் ) = ∞, போது எக்ஸ் → ∞ | |
| யூலரின் அடையாளம் | Ln (-1) = நான் π |
லோகரிதம் தயாரிப்பு விதி
X மற்றும் y இன் பெருக்கத்தின் மடக்கை என்பது x இன் மடக்கை மற்றும் y இன் மடக்கை ஆகும்.
log b ( x y ) = log b ( x ) + log b ( y )
உதாரணத்திற்கு:
பதிவு 10 (3 ∙ 7) = பதிவு 10 (3) + பதிவு 10 (7)
மடக்கை மேற்கோள் விதி
X மற்றும் y இன் பிரிவின் மடக்கை என்பது x இன் மடக்கை மற்றும் y இன் மடக்கை வேறுபாடு ஆகும்.
log b ( x / y ) = log b ( x ) - log b ( y )
உதாரணத்திற்கு:
log 10 (3 / 7) = log 10 (3) - உள்நுழைய 10 (7)
மடக்கை சக்தி விதி
Y இன் சக்திக்கு உயர்த்தப்பட்ட x இன் மடக்கை x இன் மடக்கை y மடங்கு ஆகும்.
log b ( x y ) = y log b ( x )
உதாரணத்திற்கு:
பதிவு 10 (2 8 ) = 8 ∙ பதிவு 10 (2)
இயற்கையான மடக்கைகளின் வழித்தோன்றல்
இயற்கையான மடக்கை செயல்பாட்டின் வழித்தோன்றல் பரஸ்பர செயல்பாடு ஆகும்.
எப்பொழுது
f ( x ) = ln ( x )
F (x) இன் வழித்தோன்றல்:
f ' ( x ) = 1 / x
இயற்கையான மடக்கைகளின் ஒருங்கிணைப்பு
இயற்கையான மடக்கை செயல்பாட்டின் ஒருங்கிணைப்பு பின்வருமாறு:
எப்பொழுது
f ( x ) = ln ( x )
F (x) இன் ஒருங்கிணைப்பு:
∫ ஊ ( எக்ஸ் ) டிஎக்ஸ் = ∫ Ln ( எக்ஸ் ) டிஎக்ஸ் = எக்ஸ் ∙ (Ln ( எக்ஸ் ) - 1) + சி
0 இன் Ln
பூஜ்ஜியத்தின் இயற்கையான மடக்கை வரையறுக்கப்படவில்லை:
ln (0) வரையறுக்கப்படவில்லை
X பூஜ்ஜியத்தை நெருங்கும் போது, x இன் இயற்கையான மடக்கை 0 க்கு அருகிலுள்ள வரம்பு கழித்தல் முடிவிலி:
![]()
1 இன் எல்.என்
ஒன்றின் இயல்பான மடக்கை பூஜ்ஜியமாகும்:
ln (1) = 0
முடிவிலியின் எல்.என்
முடிவிலியின் இயல்பான மடக்கைகளின் வரம்பு, x முடிவிலியை அணுகும்போது முடிவிலிக்கு சமம்:
லிம் Ln ( எக்ஸ் ) = ∞, போது எக்ஸ் → ∞
சிக்கலான மடக்கை
சிக்கலான எண் z க்கு:
z = re iθ = x + iy
சிக்கலான மடக்கை இருக்கும் (n = ...- 2, -1,0,1,2, ...):
பதிவு z = ln ( r ) + i ( θ + 2nπ ) = ln ( x ( x 2 + y 2 )) + i · arctan ( y / x ))
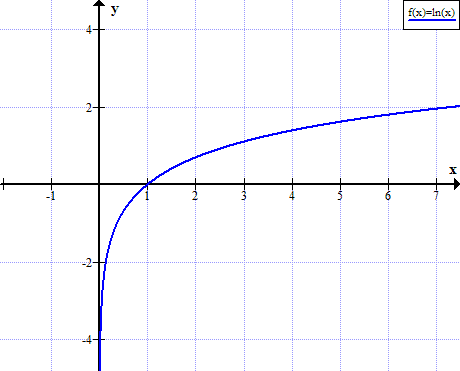
Ln (x) இன் வரைபடம்
x இன் உண்மையான நேர்மறை அல்லாத மதிப்புகளுக்கு ln (x) வரையறுக்கப்படவில்லை:
இயற்கை மடக்கை அட்டவணை
| x | ln x |
|---|---|
| 0 | வரையறுக்கப்படவில்லை |
| 0 + | - |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
மேலும் காண்க
- மடக்கை (பதிவு)
- இயற்கை மடக்கை கால்குலேட்டர்
- பூஜ்ஜியத்தின் இயற்கையான மடக்கை
- ஒன்றின் இயற்கையான மடக்கை
- மின் இயல்பான மடக்கை
- முடிவிலியின் இயற்கையான மடக்கை
- எதிர்மறை எண்ணின் இயற்கையான மடக்கை
- Ln தலைகீழ் செயல்பாடு
- ln (x) வரைபடம்
- இயற்கை மடக்கை அட்டவணை
- லோகரிதம் கால்குலேட்டர்
- e மாறிலி
இயற்கணிதம்
விரைவான அட்டவணைகள்