இணக்கம்

தலைகீழ் செயல்பாடு g (t-τ) உடன் f (τ) இன் தொடர்பு செயல்பாடு ஆகும்.

மாற்றும் ஆபரேட்டர் என்பது நட்சத்திரக் குறியீடு * .

F (t) மற்றும் g (t) ஆகியவற்றின் மாற்றம் f (τ) முறைகள் f (t-τ) இன் ஒருங்கிணைப்புக்கு சமம்:

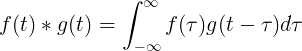
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

2 தனித்துவமான செயல்பாடுகளின் மாற்றம் பின்வருமாறு வரையறுக்கப்படுகிறது:

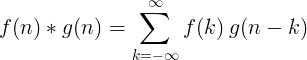
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2 பரிமாண தனித்துவமான மாற்றம் வழக்கமாக பட செயலாக்கத்திற்கு பயன்படுத்தப்படுகிறது.

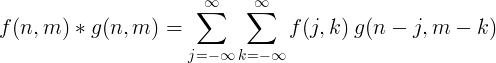
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

வெளியீட்டு சமிக்ஞை y (n) ஐப் பெற தூண்டுதல் மறுமொழி h (n) உடன் மாற்றுவதன் மூலம் தனித்துவமான உள்ளீட்டு சமிக்ஞை x (n) ஐ வடிகட்டலாம்.

y ( n ) = x ( n ) * h ( n )

2 செயல்பாடுகளின் பெருக்கத்தின் ஃபோரியர் மாற்றம் ஒவ்வொரு செயல்பாட்டின் ஃபோரியர் உருமாற்றங்களின் மாற்றத்திற்கு சமம்:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

2 செயல்பாடுகளின் மாற்றத்தின் ஃபோரியர் மாற்றம் ஒவ்வொரு செயல்பாட்டின் ஃபோரியர் உருமாற்றங்களின் பெருக்கத்திற்கு சமம்:

ℱ { f * g } = ℱ { f } ⋅ g { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( கள் ) ⋅ G ( கள் )

மேலும் காண்க