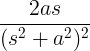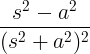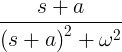லாப்லேஸ் டிரான்ஸ்ஃபார்ம்

லாப்லேஸ் உருமாற்றம் பூஜ்ஜியத்திலிருந்து முடிவிலிக்கு ஒருங்கிணைப்பதன் மூலம் நேர டொமைன் செயல்பாட்டை எஸ்-டொமைன் செயல்பாடாக மாற்றுகிறது

நேர டொமைன் செயல்பாட்டின், e ^-st ஆல் பெருக்கப்படுகிறது .

வேறுபட்ட சமன்பாடுகள் மற்றும் ஒருங்கிணைப்புகளுக்கான தீர்வுகளை விரைவாகக் கண்டுபிடிக்க லாப்லேஸ் உருமாற்றம் பயன்படுத்தப்படுகிறது.

நேர டொமைனில் உள்ள வழித்தோன்றல் கள் டொமைனில் s ஆல் பெருக்கமாக மாற்றப்படுகிறது.

நேர களத்தில் ஒருங்கிணைப்பு s- களத்தில் s ஆல் பிரிவாக மாற்றப்படுகிறது.

லேப்ளேஸ் உருமாறும் செயல்பாடு

லாப்லேஸ் மாற்றம் எல் }} ஆபரேட்டருடன் வரையறுக்கப்படுகிறது :

$F (கள்) = \ mathcal {L} \ இடது \ {f (t) \ வலது \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

தலைகீழ் லேப்ளேஸ் உருமாற்றத்தை நேரடியாக கணக்கிட முடியும்.

வழக்கமாக தலைகீழ் மாற்றம் உருமாற்ற அட்டவணையில் இருந்து வழங்கப்படுகிறது.

செயல்பாட்டு பெயர்	நேர டொமைன் செயல்பாடு	லேப்ளேஸ் உருமாற்றம்
செயல்பாட்டு பெயர்	f ( t )	F ( கள் ) = L { f ( t )}
நிலையான	1	$\ frac {1} {s}$
நேரியல்	t	$\ frac {1} {s ^ 2}$
சக்தி	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
சக்தி	t ^அ	( A +1) ⋅ s ^{- ( a +1)}
அடுக்கு	e ^இல்	$\ frac {1} {sa}$
சைன்	பாவம் மணிக்கு	$\ frac {a} {s ^ 2 + a ^ 2}$
கொசைன்	cos at	$\ frac {s} {s ^ 2 + a ^ 2}$
ஹைபர்போலிக் சைன்	at sinh	$\ frac {a} {s ^ 2-a ^ 2}$
ஹைபர்போலிக் கொசைன்	at cosh	$\ frac {s} {s ^ 2-a ^ 2}$
வளர்ந்து வரும் சைன்	டி பாவம் மணிக்கு	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
வளர்ந்து வரும் கொசைன்	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
அழுகும் சைன்	e ^-at பாவம் ωt	$\ frac {\ ஒமேகா} {\ இடது (கள் + அ \ வலது) ^ 2 + \ ஒமேகா ^ 2}$
அழுகும் கொசைன்	e ^-at cos ωt	$\ frac {s + a} {\ இடது (s + a \ வலது) ^ 2 + \ ஒமேகா ^ 2}$
டெல்டா செயல்பாடு	δ ( டி )	1
தாமதமான டெல்டா	δ ( ta )	e ^-as

சொத்தின் பெயர்	நேர டொமைன் செயல்பாடு	லேப்ளேஸ் உருமாற்றம்	கருத்து
	f ( t )	எஃப் ( கள் )
நேரியல்	af ( t ) + bg ( t )	aF ( கள் ) + பி.ஜி ( கள் )	a , b நிலையானது
அளவு மாற்றம்	f ( இல் )	$\ frac {1} {a} F \ இடது (\ frac {s} {a} \ வலது)$	a / 0
ஷிப்ட்	e ^-at f ( t )	எஃப் ( கள் + அ )
தாமதம்	f ( ta )	e ^{- என} F ( கள் )
வழித்தோன்றல்	$\ frac {df (t)} {dt}$	sF ( கள் ) - f (0)
N-th வழித்தோன்றல்	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( கள் ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
சக்தி	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (கள்)} {ds ^ n}$
ஒருங்கிணைப்பு	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (கள்)$
பரஸ்பர	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
இணக்கம்	f ( t ) * g ( t )	F ( கள் ) ⋅ G ( கள் )	* என்பது மாற்றும் ஆபரேட்டர்
அவ்வப்போது செயல்பாடு	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$