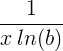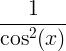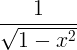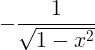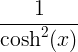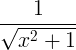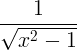வழித்தோன்றல் விதிகள்
வழித்தோன்றல் விதிகள் மற்றும் சட்டங்கள். செயல்பாடுகள் அட்டவணையின் வழித்தோன்றல்கள்.
- வழித்தோன்றல் வரையறை
- வழித்தோன்றல் விதிகள்
- செயல்பாடுகள் அட்டவணையின் வழித்தோன்றல்கள்
- வழித்தோன்றல் எடுத்துக்காட்டுகள்
வழித்தோன்றல் வரையறை
ஒரு செயல்பாட்டின் வழித்தோன்றல் என்பது x + Δx புள்ளிகளில் x (x) மற்றும் x )x உடன் x இன் செயல்பாட்டு மதிப்பின் வேறுபாட்டின் விகிதமாகும், Δx எண்ணற்ற அளவில் சிறியதாக இருக்கும்போது. வழித்தோன்றல் என்பது புள்ளி x இல் உள்ள தொடுகோட்டின் செயல்பாட்டு சாய்வு அல்லது சாய்வு ஆகும்.
![]()
இரண்டாவது வழித்தோன்றல்
இரண்டாவது வழித்தோன்றல் வழங்கியது:
![]()
அல்லது முதல் வழித்தோன்றலைப் பெறுங்கள்:
![]()
Nth வழித்தோன்றல்
N வது வழித்தோன்றல்: f (x) n முறை பெற்றுவிட்டால் கணக்கிடப்படுகிறது.
N வது வழித்தோன்றல் (N-1) வகைக்கெழுவின் வழிப்பொருளுக்கு சமமாக இருக்கும்:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
உதாரணமாக:
இன் நான்காவது வழித்தோன்றலைக் கண்டறியவும்
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
செயல்பாட்டின் வரைபடத்தில் வழித்தோன்றல்
ஒரு செயல்பாட்டின் வழித்தோன்றல் தொடுநிலை கோட்டின் சரிவு ஆகும்.
வழித்தோன்றல் விதிகள்
| வழித்தோன்றல் தொகை விதி | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| வழித்தோன்றல் தயாரிப்பு விதி | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| வழித்தோன்றல் அளவு விதி | 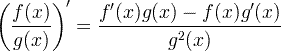 |
| வழித்தோன்றல் சங்கிலி விதி | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
வழித்தோன்றல் தொகை விதி
போது ஒரு மற்றும் ஆ மாறிலிகள் உள்ளன.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
உதாரணமாக:
இதன் வழித்தோன்றலைக் கண்டறியவும்:
3 x 2 + 4 x.
தொகை விதிப்படி:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
வழித்தோன்றல் தயாரிப்பு விதி
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
வழித்தோன்றல் அளவு விதி
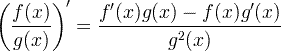
வழித்தோன்றல் சங்கிலி விதி
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
லாக்ரேஞ்சின் குறியீட்டைக் கொண்டு இந்த விதியை நன்கு புரிந்து கொள்ள முடியும்:
![]()
செயல்பாடு நேரியல் தோராயமாக்கல்
சிறிய Δx க்கு, f (x 0 + Δx) க்கு ஒரு தோராயத்தைப் பெறலாம் , f (x 0 ) மற்றும் f '(x 0 ) ஆகியவற்றை நாம் அறியும்போது :
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) x
செயல்பாடுகள் அட்டவணையின் வழித்தோன்றல்கள்
| செயல்பாட்டு பெயர் | செயல்பாடு | வழித்தோன்றல் |
|---|---|---|
| f ( x ) |
f '( x ) | |
| நிலையான | const |
0 |
| நேரியல் | x |
1 |
| சக்தி | x அ |
கோடாரி a- 1 |
| அதிவேக | e x |
e x |
| அதிவேக | ஒரு x |
a x ln a |
| இயற்கை மடக்கை | ln ( x ) |
|
| லோகரிதம் | பதிவு b ( x ) |
|
| சைன் | பாவம் x |
cos x |
| கொசைன் | cos x |
-சின் x |
| தொடுகோடு | tan x |
|
| ஆர்க்சைன் | arcsin x |
|
| ஆர்கோசின் | ஆர்கோஸ் x |
|
| ஆர்க்டாங்கென்ட் | ஆர்க்டன் x |
|
| ஹைபர்போலிக் சைன் | sinh x |
cosh x |
| ஹைபர்போலிக் கொசைன் | cosh x |
sinh x |
| ஹைபர்போலிக் தொடுகோடு | tanh x |
|
| தலைகீழ் ஹைபர்போலிக் சைன் | sinh -1 x |
|
| தலைகீழ் ஹைபர்போலிக் கொசைன் | cosh -1 x |
|
| தலைகீழ் ஹைபர்போலிக் தொடுகோடு | tanh -1 x |
|
வழித்தோன்றல் எடுத்துக்காட்டுகள்
எடுத்துக்காட்டு # 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
எடுத்துக்காட்டு # 2
f ( x ) = பாவம் (3 x 2 )
சங்கிலி விதியைப் பயன்படுத்தும்போது:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
இரண்டாவது வழித்தோன்றல் சோதனை
ஒரு செயல்பாட்டின் முதல் வழித்தோன்றல் புள்ளி x 0 இல் பூஜ்ஜியமாக இருக்கும்போது .
f '( x 0 ) = 0
புள்ளி x 0 , f '' (x 0 ) இல் உள்ள இரண்டாவது வழித்தோன்றல் , அந்த புள்ளியின் வகையைக் குறிக்கலாம்:
| f '' ( x 0 )/ 0 |
உள்ளூர் குறைந்தபட்சம் |
| f '' ( x 0 ) <0 |
உள்ளூர் அதிகபட்சம் |
| f '' ( x 0 ) = 0 |
தீர்மானிக்கப்படாதது |
மேலும் காண்க
கால்குலஸ்
- அளவு
- வழித்தோன்றல்
- ஒருங்கிணைந்த
- தொடர்
- லேப்ளேஸ் உருமாற்றம்
- இணக்கம்
- கால்குலஸ் சின்னங்கள்
விரைவான அட்டவணைகள்