อินทิกรัล

การรวมคือการดำเนินการย้อนกลับของการได้มา

อินทิกรัลของฟังก์ชันคือพื้นที่ใต้กราฟของฟังก์ชัน

นิยามเชิงปริพันธ์ไม่แน่นอน

เมื่อไหร่ dF (x) / dx = f (x) =/ ปริพันธ์ (f (x) * dx) = F (x) + c

คุณสมบัติเชิงปริพันธ์ไม่แน่นอน

อินทิกรัล (f (x) + g (x)) * dx = อินทิกรัล (f (x) * dx) + อินทิกรัล (g (x) * dx)

อินทิกรัล (a * f (x) * dx) = a * อินทิกรัล (f (x) * dx)

อินทิกรัล (f (a * x) * dx) = 1 / a * F (a * x) + c

อินทิกรัล (f (x + b) * dx) = F (x + b) + c

อินทิกรัล (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

อินทิกรัล (df (x) / dx * dx) = f (x)

การเปลี่ยนแปลงตัวแปรการรวม

เมื่อไหร่x = g (เสื้อ) และdx = g '(เสื้อ) * dt

อินทิกรัล (f (x) * dx) = ปริพันธ์ (f (g (t)) * g '(t) * dt)

การบูรณาการตามส่วนต่างๆ

อินทิกรัล (f (x) * g '(x) * dx) = f (x) * g (x) - อินทิกรัล (f' (x) * g (x) * dx)

ตารางปริพันธ์

อินทิกรัล (f (x) * dx = F (x) + c

อินทิกรัล (a * dx) = a * x + c

อินทิกรัล (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c เมื่อ a </ - 1

อินทิกรัล (1 / x * dx) = ln (abs (x)) + c

อินทิกรัล (e ^ x * dx) = e ^ x + c

อินทิกรัล (a ^ x * dx) = a ^ x / ln (x) + c

อินทิกรัล (ln (x) * dx) = x * ln (x) - x + c

อินทิกรัล (sin (x) * dx) = -cos (x) + c

อินทิกรัล (cos (x) * dx) = sin (x) + c

อินทิกรัล (tan (x) * dx) = -ln (abs (cos (x))) + c

อินทิกรัล (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

อินทิกรัล (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

อินทิกรัล (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

อินทิกรัล (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

อินทิกรัล (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

อินทิกรัล (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

อินทิกรัล (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

อินทิกรัล (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

อินทิกรัล (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

อินทิกรัล (sinh (x) * dx) = cosh (x) + c

อินทิกรัล (cosh (x) * dx) = sinh (x) + c

ปริพันธ์ (tanh (x) * dx) = ln (cosh (x)) + c

 

นิยามอินทิกรัลที่ชัดเจน

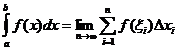
ปริพันธ์ (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i))) 

เมื่อไหร่x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

การคำนวณอินทิกรัลที่แน่นอน

เมื่อไหร่ ,

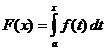 dF (x) / dx = f (x) และ

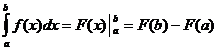
อินทิกรัล (a..b, f (x) * dx) = F (b) - F (a) 

คุณสมบัติเชิงปริพันธ์ที่แน่นอน

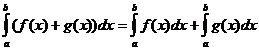
อินทิกรัล (a..b, (f (x) + g (x)) * dx) = อินทิกรัล (a..b, f (x) * dx) + อินทิกรัล (a..b, g (x) * dx )

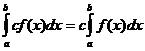
อินทิกรัล (a..b, c * f (x) * dx) = c * อินทิกรัล (a..b, f (x) * dx)

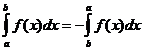
ปริพันธ์ (a..b, f (x) * dx) = - ปริพันธ์ (b..a, f (x) * dx)

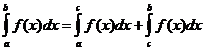
อินทิกรัล (a..b, f (x) * dx) = ปริพันธ์ (a..c, f (x) * dx) + อินทิกรัล (c..b, f (x) * dx)

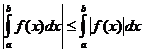
abs (อินทิกรัล (a..b, f (x) * dx)) <= อินทิกรัล (a..b, abs (f (x)) * dx)

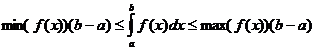นาที (f (x)) * (ba) <= ปริพันธ์ (a..b, f (x) * dx) <= สูงสุด (f (x)) * (ba) เมื่อไหร่x สมาชิกของ [a, b]

การเปลี่ยนแปลงตัวแปรการรวม

เมื่อไหร่x = g (เสื้อ) ,dx = g '(เสื้อ) * dt ,g (อัลฟา) = ก ,g (เบต้า) = b

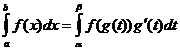
ปริพันธ์ (a..b, f (x) * dx) = ปริพันธ์ (alpha..beta, f (g (t)) * g '(t) * dt)

การบูรณาการตามส่วนต่างๆ

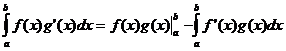
อินทิกรัล (a..b, f (x) * g '(x) * dx) = ปริพันธ์ (a..b, f (x) * g (x) * dx) - อินทิกรัล (a..b, f' (x) * ก (x) * dx)

ทฤษฎีบทค่าเฉลี่ย

เมื่อf ( x )ต่อเนื่องจะมีจุดc เป็นสมาชิกของ [a, b] ดังนั้น

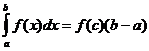
อินทิกรัล (a..b, f (x) * dx) = f (c) * (ba)  

การประมาณรูปสี่เหลี่ยมคางหมูของอินทิกรัลที่ชัดเจน

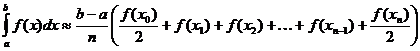
อินทิกรัล (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

ฟังก์ชันแกมมา

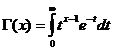
แกมมา (x) = ปริพันธ์ (0..inf, t ^ (x-1) * e ^ (- t) * dt

ฟังก์ชันแกมมาเป็นที่บรรจบกันสำหรับx/ 0

คุณสมบัติของฟังก์ชันแกมมา

G ( x +1) = x G ( x )

G ( n +1) = n ! , เมื่อ n ℕ (จำนวนเต็มบวก)เป็นสมาชิกของ

ฟังก์ชันเบต้า

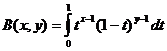
B (x, y) = ปริพันธ์ (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

ความสัมพันธ์ของฟังก์ชันเบต้าและฟังก์ชันแกมมา

B (x, y) = แกมมา (x) * แกมมา (y) / แกมมา (x + y)

 

 

 

แคลคูลัส
ตารางอย่างรวดเร็ว