ความแปรปรวน

ในความน่าจะเป็นและสถิติความแปรปรวนของตัวแปรสุ่มคือค่าเฉลี่ยของระยะห่างกำลังสองจากค่าเฉลี่ย แสดงถึงวิธีการกระจายตัวแปรสุ่มใกล้ค่าเฉลี่ย ความแปรปรวนขนาดเล็กบ่งชี้ว่าตัวแปรสุ่มมีการกระจายใกล้ค่าเฉลี่ย ความแปรปรวนขนาดใหญ่บ่งชี้ว่าตัวแปรสุ่มกระจายอยู่ไกลจากค่าเฉลี่ย ตัวอย่างเช่นเมื่อมีการแจกแจงแบบปกติเส้นโค้งระฆังแคบจะมีความแปรปรวนน้อยและเส้นโค้งระฆังกว้างจะมีความแปรปรวนมาก

นิยามความแปรปรวน

ความแปรปรวนของตัวแปรสุ่ม X คือค่าที่คาดหวังของกำลังสองของความแตกต่างของ X และค่าที่คาดหวังμ

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

จากนิยามของความแปรปรวนเราจะได้

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

ความแปรปรวนของตัวแปรสุ่มแบบต่อเนื่อง

สำหรับตัวแปรสุ่มแบบต่อเนื่องที่มีค่าเฉลี่ยμและฟังก์ชันความหนาแน่นของความน่าจะเป็น f (x):

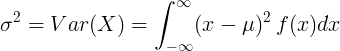
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

หรือ

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

ความแปรปรวนของตัวแปรสุ่มแบบไม่ต่อเนื่อง

สำหรับตัวแปรสุ่มแบบไม่ต่อเนื่อง X ที่มีค่าเฉลี่ยμและฟังก์ชันมวลความน่าจะเป็น P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

หรือ

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

คุณสมบัติของความแปรปรวน

เมื่อ X และ Y เป็นตัวแปรสุ่มอิสระ:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

ค่าเบี่ยงเบนมาตรฐาน►

 

ดูสิ่งนี้ด้วย

ความน่าจะเป็นและสถิติ
ตารางอย่างรวดเร็ว