การกระจายความน่าจะเป็น
ในความน่าจะเป็นและสถิติการกระจายเป็นลักษณะของตัวแปรสุ่มอธิบายความน่าจะเป็นของตัวแปรสุ่มในแต่ละค่า
การแจกแจงแต่ละรายการมีฟังก์ชันความหนาแน่นของความน่าจะเป็นและฟังก์ชันการแจกแจงความน่าจะเป็น
แม้ว่าการแจกแจงความน่าจะเป็นจะมีจำนวนไม่แน่นอน แต่ก็มีการแจกแจงทั่วไปหลายแบบที่ใช้อยู่
ฟังก์ชันการแจกแจงสะสม
การแจกแจงความน่าจะเป็นอธิบายโดยฟังก์ชันการแจกแจงสะสม F (x)
ซึ่งเป็นความน่าจะเป็นของตัวแปรสุ่ม X ที่จะได้รับค่าที่น้อยกว่าหรือเท่ากับ x:
F ( x ) = P ( X ≤ x )
การกระจายอย่างต่อเนื่อง
ฟังก์ชันการแจกแจงสะสม F (x) คำนวณโดยการรวมฟังก์ชันความหนาแน่นของความน่าจะเป็น f (u) ของตัวแปรสุ่มต่อเนื่อง X

การกระจายแบบไม่ต่อเนื่อง
ฟังก์ชันการแจกแจงสะสม F (x) คำนวณโดยผลรวมของฟังก์ชันมวลความน่าจะเป็น P (u) ของตัวแปรสุ่มแบบไม่ต่อเนื่อง X
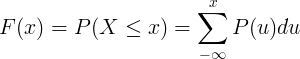
ตารางการแจกแจงแบบต่อเนื่อง
การแจกแจงแบบต่อเนื่องคือการแจกแจงของตัวแปรสุ่มแบบต่อเนื่อง
ตัวอย่างการแจกแจงแบบต่อเนื่อง
...
ตารางการแจกแจงแบบต่อเนื่อง
| ชื่อการจัดจำหน่าย | สัญลักษณ์การกระจาย | ฟังก์ชันความหนาแน่นของความน่าจะเป็น (pdf) | ค่าเฉลี่ย | ความแปรปรวน |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| ปกติ / เกาส์เซียน | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| เครื่องแบบ | X ~ U ( ก , ข ) |
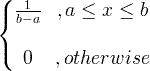 |
|
|
| เอกซ์โปเนนเชียล | X ~ exp (λ) | |
|
|
| แกมมา | X ~ แกมมา ( c , λ) | 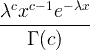 x / 0, c / 0, λ/ 0 |
|
|
| ไคสแควร์ | X ~ χ 2 ( k ) |
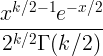 |
k |
2 k |
| วิสฮาร์ท | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| เบต้า | ||||
| ไวบุล | ||||
| เข้าสู่ระบบปกติ | X ~ LN (μ, σ 2 ) |
|||
| เรย์ลี | ||||
| Cauchy | ||||
| ไดริชเล็ต | ||||
| Laplace | ||||
| เลวี่ | ||||
| ข้าว | ||||
| นักศึกษาม |
ตารางการแจกแจงแบบไม่ต่อเนื่อง
การแจกแจงแบบไม่ต่อเนื่องคือการแจกแจงของตัวแปรสุ่มแบบไม่ต่อเนื่อง
ตัวอย่างการแจกแจงแบบไม่ต่อเนื่อง
...
ตารางการแจกแจงแบบไม่ต่อเนื่อง
| ชื่อการจัดจำหน่าย | สัญลักษณ์การกระจาย | ฟังก์ชันมวลความน่าจะเป็น (pmf) | ค่าเฉลี่ย | ความแปรปรวน | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| ทวินาม | X ~ ถัง ( n , p ) |
|
np |
np (1- พี ) |
|
| ปัวซอง | X ~ ปัวซอง (λ) |
|
λ≥ 0 |
λ |
λ |
| เครื่องแบบ | X ~ U ( ก, ข ) |
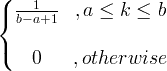 |
|
|
|
| เรขาคณิต | X ~ Geom ( p ) |
|
|
|
|
| ไฮเปอร์เรขาคณิต | X ~ HG ( N , K , n ) |
 |
N = 0,1,2, ... K = 0,1, .. , N n = 0,1, ... , N |
|
|
| เบอร์นูลลี | X ~ เบิร์น ( p ) |
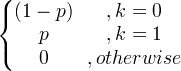 |
p |
p (1- หน้า ) |
|
ดูสิ่งนี้ด้วย
ความน่าจะเป็นและสถิติ
- ความน่าจะเป็นพื้นฐาน
- ความคาดหวัง
- ความแปรปรวน
- ส่วนเบี่ยงเบนมาตรฐาน
- การกระจายความน่าจะเป็น
- การแจกแจงปกติ
- สัญลักษณ์สถิติ
ตารางอย่างรวดเร็ว