Pamamahagi ng Probabilidad

Sa posibilidad at pamamahagi ng mga istatistika ay isang katangian ng isang random variable, inilalarawan ang posibilidad ng random variable sa bawat halaga.

Ang bawat pamamahagi ay may isang tiyak na pagpapaandar density density at posibilidad ng pagpapaandar function.

Bagaman mayroong walang katiyakan na bilang ng mga pamamahagi ng posibilidad, maraming mga karaniwang pamamahagi ang ginagamit.

Cumulative function ng pamamahagi

Ang pamamahagi ng posibilidad ay inilarawan ng pinagsamang pagpapaandar na pagpapaandar F (x),

alin ang posibilidad ng random variable X upang makuha ang halaga na mas maliit sa o katumbas ng x:

F ( x ) = P ( X ≤ x )

Patuloy na pamamahagi

Ang pinagsama-samang function ng pamamahagi F (x) ay kinakalkula sa pamamagitan ng pagsasama ng posibilidad ng pag-andar ng density f (u) ng tuluy-tuloy na random variable X.

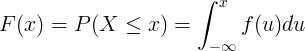
Discrete pamamahagi

Ang pinagsama-samang function ng pamamahagi F (x) ay kinakalkula sa pamamagitan ng pagbubuod ng posibilidad ng pagpapaandar ng mass P (u) ng discrete random variable X.

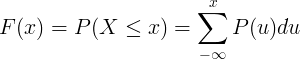
Patuloy na talahanayan ng mga pamamahagi

Ang tuluy-tuloy na pamamahagi ay ang pamamahagi ng isang tuloy-tuloy na random variable.

Patuloy na halimbawa ng pamamahagi

...

Patuloy na talahanayan ng mga pamamahagi

Pangalan ng pamamahagi Simbolo ng pamamahagi Pag-andar ng density ng probabilidad (pdf) Ibig sabihin Pagkakaiba-iba
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussian

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniporme

X ~ U ( a , b )

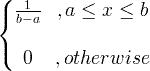 \ simulan ang {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, kung hindi man tapusin ang {matrix} \ frac {(ba) ^ 2} {12}
Exponential X ~ exp (λ) \ simulan ang {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 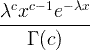\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi square

X ~ χ 2 ( k )

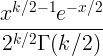 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Levy        
Bigas        
Mag-aaral t        

Talaan ng discrete na pamamahagi

Ang discrete pamamahagi ay ang pamamahagi ng isang discrete random variable.

Discrete halimbawa ng pamamahagi

...

Talaan ng discrete na pamamahagi

Pangalan ng pamamahagi Simbolo ng pamamahagi Pag-andar ng mass probabilidad (pmf) Ibig sabihin Pagkakaiba-iba
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomial

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ
Uniporme

X ~ U ( a, b )

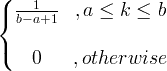 \ simulan ang {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, kung hindi man tapusin ang {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometric

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hyper-geometric

X ~ HG ( N , K , n )

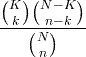N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Bern ( p )

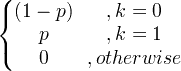 \ simulan ang {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, kung hindi man \ end {matrix}

p

p (1- p )

 

Tingnan din

PROBABILITY & STATISTICS
RAPID TABLES