Karaniwang lihis

Sa posibilidad at istatistika, ang karaniwang paglihis ng isang random variable ay ang average na distansya ng isang random variable mula sa average na halaga.

Kinakatawan nito kung paano ipinamamahagi ang random variable malapit sa average na halaga. Ang maliit na standard na paglihis ay nagpapahiwatig na ang random na variable ay ipinamamahagi malapit sa average na halaga. Ang malaking pamantayang paglihis ay nagpapahiwatig na ang random variable ay ipinamamahagi nang malayo sa ibig sabihin ng halaga.

Karaniwang pormula sa kahulugan ng paglihis

Ang karaniwang paglihis ay ang parisukat na ugat ng pagkakaiba-iba ng random variable X, na may average na halaga ng μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Mula sa kahulugan ng karaniwang paglihis na maaari nating makuha

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Karaniwang paglihis ng tuluy-tuloy na random variable

Para sa tuluy-tuloy na variable ng variable na may average na halaga μ at posibilidad ng pagpapaandar ng density f (x):

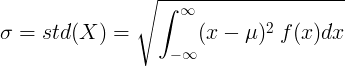
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

o

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ kanan] - \ mu ^ 2}

Karaniwang paglihis ng discrete random variable

Para sa discrete random variable X na may average na halaga μ at posibilidad ng pagpapaandar ng mass P (x):

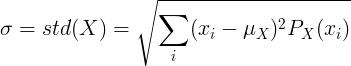
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

o

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ kanan] - \ mu ^ 2}

 

Pamamahagi ng posibilidad ►

 

Tingnan din

PROBABILITY & STATISTICS
RAPID TABLES