Evrişim
Evrişim, f (τ) 'nin ters fonksiyon g (t-τ) ile korelasyon fonksiyonudur.
Evrişim operatörü yıldız işaretidir * .
Sürekli evrişim
F (t) ve g (t) 'nin evrişimi f (τ) çarpı f (t-τ) nin integraline eşittir:
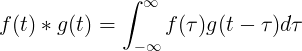
Ayrık evrişim
2 ayrık fonksiyonun evrişimi şu şekilde tanımlanır:
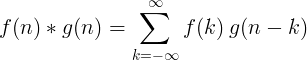
2D ayrık evrişim
2 boyutlu ayrık evrişim genellikle görüntü işleme için kullanılır.
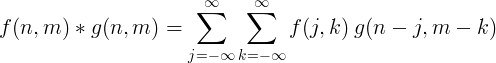
Evrişimli filtre uygulaması
Çıktı sinyalini y (n) elde etmek için ayrık giriş sinyalini x (n) dürtü yanıtı h (n) ile evrişim yoluyla filtreleyebiliriz.
y ( n ) = x ( n ) * h ( n )
Evrişim teoremi
2 fonksiyonun çarpımının Fourier dönüşümü, her fonksiyonun Fourier dönüşümlerinin evrişimine eşittir:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
2 fonksiyonun bir evrişiminin Fourier dönüşümü, her fonksiyonun Fourier dönüşümlerinin çarpımına eşittir:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Sürekli Fourier dönüşümü için evrişim teoremi
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Ayrık Fourier dönüşümü için evrişim teoremi
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Laplace dönüşümü için evrişim teoremi
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )