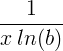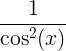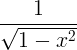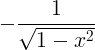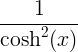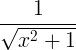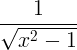Türev kuralları

Türev kurallar ve kanunlar. Fonksiyonların türevleri tablosu.

Türev tanımı
Türev kuralları
Fonksiyonların türevleri tablosu
Türev örnekler

Türev tanımı

Bir fonksiyonun türevi, Δx sonsuz derecede küçük olduğunda, x + Δx ve x ile x noktalarındaki f (x) fonksiyon değerinin farkının oranıdır. Türev, x noktasındaki teğet doğrunun fonksiyon eğimi veya eğimidir.

$f '(x) = \ lim _ {\ Delta x \ ila 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}$

İkinci türev

İkinci türev şu şekilde verilir:

Veya basitçe ilk türevi türetin:

N. türev

N inci türevi f (x) n-kere türetmek hesaplanır.

N inci türevi (n-1) türevi türev için eşit:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Misal:

Dördüncü türevini bulun

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

Fonksiyonun grafiğinde türev

Bir fonksiyonun türevi, teğet doğrunun eğimidir.

Türev kuralları

Türev toplam kuralı	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Türev ürün kuralı	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Türev bölüm kuralı	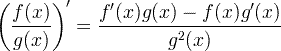$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$
Türev zincir kuralı	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Türev toplam kuralı

Ne zaman bir ve b sabitlerdir.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Misal:

Türevini bulun:

3 x ² + 4 x.

Toplam kuralına göre:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Türev ürün kuralı

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Türev bölüm kuralı

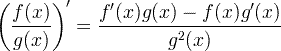
$\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}$

Türev zincir kuralı

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Bu kural, Lagrange gösterimi ile daha iyi anlaşılabilir:

$\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}$

Fonksiyon doğrusal yaklaşım

Küçük Δx için, f (x ₀ ) ve f '(x ₀ ) ' ı bildiğimizde, f (x ₀ + Δx) 'e bir yaklaşım elde edebiliriz :

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Fonksiyonların türevleri tablosu

Fonksiyon adı	Fonksiyon	Türev
Fonksiyon adı	f ( x )	f '( x )
Sabit	sabit	0
Doğrusal	x	1
Güç	x ^a	balta ^a-¹
Üstel	e ^x	e ^x
Üstel	bir ^x	a ^x ln a
Doğal logaritma	ln ( x )
Logaritma	günlük _b ( x )
Sinüs	günah x	çünkü x
Kosinüs	çünkü x	-sin x
Teğet	tan x
Arcsine	arcsin x
Arkkosin	arccos x
Arktanjant	arctan x
Hiperbolik sinüs	sinh x	cosh x
Hiperbolik kosinüs	cosh x	sinh x
Hiperbolik tanjant	tanh x
Ters hiperbolik sinüs	sinh ^-1 x
Ters hiperbolik kosinüs	cosh ^-1 x
Ters hiperbolik tanjant	tanh ^-1 x