Квадратне рівняння
Квадратне рівняння - це поліном другого порядку з 3 коефіцієнтами - a , b , c .
Квадратне рівняння задається:
сокира 2 + bx + c = 0
Рішення квадратного рівняння задається 2 числами х 1 і х 2 .
Ми можемо змінити квадратне рівняння на вигляд:
( x - x 1 ) ( x - x 2 ) = 0
Квадратична формула
Рішення квадратного рівняння задається квадратною формулою:
![]()
Вираз усередині квадратного кореня називається дискримінантним і позначається Δ:
Δ = b 2 - 4 змінного струму
Квадратична формула з дискримінантними позначеннями:
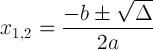
Цей вираз важливий, оскільки він може розповісти нам про рішення:
- Коли Δ/ 0, є 2 дійсних корені x 1 = (- b + √ Δ ) / (2a) та x 2 = (- b-√ Δ ) / (2a) .
- Коли Δ = 0, є один корінь x 1 = x 2 = -b / (2a) .
- При Δ <0, немає дійсних коренів, є 2 комплексні корені:
х 1 = (- Ь + i√ -Δ ) / (2а) і х 2 = (- bi√ -Δ ) / (2a) .
Проблема No1
3 х 2 +5 х +2 = 0
рішення:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Проблема No2
3 x 2 -6 x +3 = 0
рішення:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Проблема No3
x 2 +2 x +5 = 0
рішення:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Реальних рішень немає. Значення є комплексними числами:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Квадратичний графік функції
Квадратична функція - це поліноміальна функція другого порядку:
f ( x ) = ax 2 + bx + c
Рішеннями квадратного рівняння є корені квадратної функції, які є точками перетину графіка квадратної функції з віссю x, коли
f ( x ) = 0
Коли є 2 точки перетину графіка з віссю х, є 2 рішення квадратного рівняння.
Коли є 1 точка перетину графіка з віссю х, є 1 рішення квадратного рівняння.
Коли немає точок перетину графіка з віссю х, ми отримуємо не реальні рішення (або 2 комплексних рішення).