Натуральний логарифм - ln (x)

Натуральний логарифм - це логарифм основи е числа.

• Визначення природного логарифму (ln)
• Правила та властивості природного логарифму (ln)
  • Похідна натурального логарифму (ln)
  • Інтеграл природного логарифму (ln)
• Складний логарифм
• Графік ln (x)
• Таблиця натуральних логарифмів (ln)
• Калькулятор природного логарифму

Визначення натурального логарифму

Коли

e ^y = x

Тоді основа e е логарифмом x

ln ( x ) = log _e ( x ) = y

 

Е константа або число Ейлера:

e ≈ 2,71828183

Ln як обернена функція експоненціальної функції

Функція натурального логарифму ln (x) є оберненою функцією експоненціальної функції e ^x .

При x/ 0,

f ( f ^-1 ( x )) = e ^{ln ( x )} = x

Або

f ^-1 ( f ( x )) = ln ( e ^x ) = x

Правила та властивості природного логарифму

Назва правила	Правило	Приклад
Правило продукту	ln ( x ∙ y ) = ln ( x ) + ln ( y )	ln (3 ∙ 7) = ln (3) + ln (7)
Правило частки	ln ( x / y ) = ln ( x ) - ln ( y )	Ln (3 / 7) = Ln (3) - п (7)
Правило влади	ln ( x y ) = y ∙ ln ( x )	ln (2 8 ) = 8 ∙ ln (2)
ln похідна	f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x
В цілому	∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
ln від'ємного числа	ln ( x ) не визначено, коли x ≤ 0
нуль	ln (0) не визначено
ln одного	ln (1) = 0
ln нескінченності	lim ln ( x ) = ∞, коли x → ∞
Особа Ейлера	ln (-1) = i π

 

Правило добутку логарифму

Логарифм множення x та y - це сума логарифму x та логарифму y.

log _b ( x ∙ y ) = log _b ( x ) + log _b ( y )

Наприклад:

log ₁₀ (3 ∙ 7) = log ₁₀ (3) + log ₁₀ (7)

Правило частки логарифму

Логарифм поділу x та y - це різниця логарифму x та логарифму y.

log _b ( x / y ) = log _b ( x ) - log _b ( y )

Наприклад:

увійти ₁₀ (3 / 7) = увійти ₁₀ (3) - увійти в ₁₀ (7)

Правило степеня логарифму

Логарифм x, піднятий до степеня y, у помножений на логарифм x.

log _b ( x ^y ) = y ∙ log _b ( x )

Наприклад:

log ₁₀ (2 ⁸ ) = 8 ∙ log ₁₀ (2)

Похідна натурального логарифму

Похідною функції натурального логарифму є зворотна функція.

Коли

f ( x ) = ln ( x )

Похідною f (x) є:

f ' ( x ) = 1 / x

Інтеграл природного логарифму

Інтеграл функції натурального логарифму задається:

Коли

f ( x ) = ln ( x )

Інтегралом f (x) є:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln від 0

Природний логарифм нуля не визначений:

ln (0) не визначено

Межа поблизу 0 натурального логарифму x, коли x наближається до нуля, дорівнює мінус нескінченності:

Ln з 1

Натуральний логарифм одиниці дорівнює нулю:

ln (1) = 0

Ln нескінченності

Межа природного логарифму нескінченності, коли x наближається до нескінченності, дорівнює нескінченності:

lim ln ( x ) = ∞, коли x → ∞

Складний логарифм

Для комплексного числа z:

z = re ^iθ = x + iy

Складний логарифм буде (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x ² + y ² )) + i · арктан ( y / x ))

Графік ln (x)

ln (x) не визначено для дійсних непозитивних значень x:

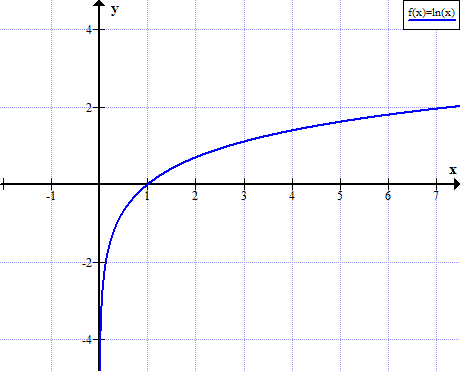
Таблиця натуральних логарифмів

х	ln x
0	невизначений
0 +	- ∞
0,0001	-9,210340
0,001	-6,907755
0,01	-4.605170
0,1	-2.302585
1	0
2	0,693147
e ≈ 2,7183	1
3	1,098612
4	1.386294
5	1,609438
6	1,791759
7	1,945910
8	2.079442
9	2,197225
10	2,302585
20	2,995732
30	3,401197
40	3,688879
50	3,912023
60	4.094345
70	4.248495
80	4.382027
90	4,499810
100	4,605170
200	5.298317
300	5.703782
400	5.991465
500	6,214608
600	6,396930
700	6,551080
800	6,684612
900	6,802395
1000	6,907755
10000	9.210340

 

Правила логарифму ►

 

---

Дивіться також

• Логарифм (журнал)
• Калькулятор природного логарифму
• Натуральний логарифм нуля
• Натуральний логарифм одиниці
• Натуральний логарифм e
• Природний логарифм нескінченності
• Натуральний логарифм від’ємного числа
• Ln обернена функція
• Графік ln (x)
• Таблиця натурального логарифму
• Калькулятор логарифмів
• e константа