Правила логарифму
База б логарифм ряду є показником , що нам потрібно , щоб підняти базу для того , щоб отримати номер.
- Визначення логарифму
- Правила логарифму
- Задачі на логарифм
- Складний логарифм
- Графік журналу (x)
- Таблиця логарифмів
- Калькулятор логарифмів
Визначення логарифму
Коли b піднято в ступінь y дорівнює x:
b y = x
Тоді базовий b логарифм x дорівнює y:
log b ( x ) = y
Наприклад, коли:
2 4 = 16
Тоді
журнал 2 (16) = 4
Логарифм як обернена функція експоненціальної функції
Логарифмічна функція,
y = log b ( x )
- обернена функція експоненціальної функції,
x = b y
Отже, якщо ми обчислимо експоненційну функцію логарифму x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Або якщо ми обчислимо логарифм експоненціальної функції x,
f -1 ( f ( x )) = log b ( b x ) = x
Натуральний логарифм (ln)
Натуральний логарифм - це логарифм до основи e:
ln ( x ) = log e ( x )
Коли e константа - це число:
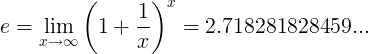
або
![]()
Див .: Природний логарифм
Обчислення зворотного логарифму
Обернений логарифм (або антилогарифм) обчислюється шляхом підняття основи b до логарифму y:
x = log -1 ( y ) = b y
Логарифмічна функція
Логарифмічна функція має основну форму:
f ( x ) = log b ( x )
Правила логарифму
| Назва правила | Правило |
|---|---|
Правило добутку логарифму |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Правило частки логарифму |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Правило степеня логарифму |
log b ( x y ) = y ∙ log b ( x ) |
Правило базового перемикача логарифму |
log b ( c ) = 1 / log c ( b ) |
Правило зміни базису логарифму |
log b ( x ) = log c ( x ) / log c ( b ) |
Похідна логарифму |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Інтеграл логарифму |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Логарифм від’ємного числа |
log b ( x ) не визначено, коли x ≤ 0 |
Логарифм 0 |
log b (0) не визначено |
Логарифм 1 |
log b (1) = 0 |
Логарифм основи |
log b ( b ) = 1 |
Логарифм нескінченності |
lim log b ( x ) = ∞, коли x → ∞ |
Див .: Правила логарифму
Правило добутку логарифму
Логарифм множення x та y - це сума логарифму x та логарифму y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Наприклад:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Правило частки логарифму
Логарифм поділу x та y - це різниця логарифму x та логарифму y.
log b ( x / y ) = log b ( x ) - log b ( y )
Наприклад:
увійти 10 (3 / 7) = увійти 10 (3) - увійти в 10 (7)
Правило степеня логарифму
Логарифм x, піднятий до степеня y, у помножений на логарифм x.
log b ( x y ) = y ∙ log b ( x )
Наприклад:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Правило базового перемикача логарифму
Логарифм базису b дорівнює 1, поділений на логарифм базису b.
log b ( c ) = 1 / log c ( b )
Наприклад:
log 2 (8) = 1 / log 8 (2)
Правило зміни базису логарифму
Базовий логарифм b x - це базовий c логарифм x, поділений на базовий c логарифм b.
log b ( x ) = log c ( x ) / log c ( b )
Наприклад, для обчислення журналу 2 (8) в калькуляторі нам потрібно змінити базу на 10:
log 2 (8) = log 10 (8) / log 10 (2)
Див .: правило зміни журналу
Логарифм від’ємного числа
Реальний логарифм базису x, коли x <= 0, не визначений, коли x від’ємне або дорівнює нулю:
log b ( x ) не визначено, коли x ≤ 0
Див .: журнал від’ємного числа
Логарифм 0
Базовий логарифм нуля невизначений:
log b (0) не визначено
Межа базового b логарифму x, коли x наближається до нуля, дорівнює мінус нескінченності:
![]()
Див .: журнал нуля
Логарифм 1
Логарифм основи b одиниці дорівнює нулю:
log b (1) = 0
Наприклад, базовий два логарифми одиниці дорівнює нулю:
log 2 (1) = 0
Див .: журнал одного
Логарифм нескінченності
Межа базового логарифму b для x, коли x наближається до нескінченності, дорівнює нескінченності:
lim log b ( x ) = ∞, коли x → ∞
Див .: журнал нескінченності
Логарифм основи
Основний b-логарифм b один:
log b ( b ) = 1
Наприклад, базовий два логарифм з двох дорівнює одному:
log 2 (2) = 1
Похідна логарифму
Коли
f ( x ) = log b ( x )
Тоді похідна від f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Див .: похідна журналу
Інтеграл логарифму
Інтеграл логарифму x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Наприклад:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Наближення логарифму
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Складний логарифм
Для комплексного числа z:
z = re iθ = x + iy
Складний логарифм буде (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · арктан ( y / x ))
Задачі та відповіді на логарифми
Проблема No1
Знайдіть x для
log 2 ( x ) + log 2 ( x -3) = 2
Рішення:
Використовуючи правило товару:
log 2 ( x ∙ ( x -3)) = 2
Зміна форми логарифму відповідно до визначення логарифму:
x ∙ ( x -3) = 2 2
Або
х 2 -3 х -4 = 0
Розв’язування квадратного рівняння:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Оскільки логарифм не визначений для від’ємних чисел, відповідь така:
х = 4
Проблема No2
Знайдіть x для
log 3 ( x +2) - log 3 ( x ) = 2
Рішення:
Використовуючи правило частки:
журнал 3 (( x +2) / x ) = 2
Зміна форми логарифму відповідно до визначення логарифму:
( x +2) / x = 3 2
Або
x +2 = 9 x
Або
8 х = 2
Або
x = 0,25
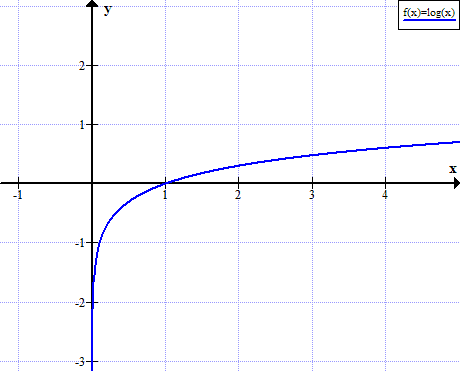
Графік журналу (x)
log (x) не визначено для дійсних непозитивних значень x:
Таблиця логарифмів
| х | журнал 10 х | журнал 2 х | log e x |
|---|---|---|---|
| 0 | невизначений | невизначений | невизначений |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6,643856 | -4.605170 |
| 0,1 | -1 | -3,321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,477121 | 1,584963 | 1,098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2,321928 | 1,609438 |
| 6 | 0,778151 | 2,584963 | 1,791759 |
| 7 | 0,845098 | 2,807355 | 1,945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0,954243 | 3,169925 | 2,197225 |
| 10 | 1 | 3,321928 | 2,302585 |
| 20 | 1.301030 | 4,321928 | 2,995732 |
| 30 | 1.477121 | 4,906891 | 3,401197 |
| 40 | 1,602060 | 5,321928 | 3,688879 |
| 50 | 1,698970 | 5.643856 | 3,912023 |
| 60 | 1,7778151 | 5,906991 | 4.094345 |
| 70 | 1,845098 | 6.129283 | 4.248495 |
| 80 | 1,903090 | 6,321928 | 4.382027 |
| 90 | 1,954243 | 6.491853 | 4,499810 |
| 100 | 2 | 6,643856 | 4,605170 |
| 200 | 2,301030 | 7,643856 | 5.298317 |
| 300 | 2.477121 | 8,228819 | 5.703782 |
| 400 | 2,602060 | 8,643856 | 5.991465 |
| 500 | 2,698970 | 8,965784 | 6,214608 |
| 600 | 2,7778151 | 9,228819 | 6,396930 |
| 700 | 2,845098 | 9,451211 | 6,551080 |
| 800 | 2,903090 | 9,643856 | 6,684612 |
| 900 | 2,954243 | 9,813781 | 6,802395 |
| 1000 | 3 | 9,965784 | 6,907755 |
| 10000 | 4 | 13,287712 | 9.210340 |
Дивіться також
- Правила логарифму
- Зміна логарифму основи
- Логарифм нуля
- Логарифм одиниці
- Логарифм нескінченності
- Логарифм від’ємного числа
- Калькулятор логарифмів
- Графік логарифму
- Таблиця логарифмів
- Калькулятор природного логарифму
- Натуральний логарифм - ln x
- e константа
- Децибел (дБ)