Виток

Конволюція - це кореляційна функція f (τ) із оберненою функцією g (t-τ).

Оператором згортки є символ зірочки * .

Звитка f (t) та g (t) дорівнює інтегралу f (τ), помноженому на f (t-τ):

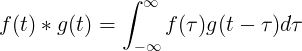
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Скрутка 2 дискретних функцій визначається як:

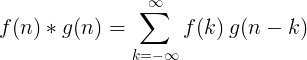
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

Двовимірна дискретна згортка зазвичай використовується для обробки зображень.

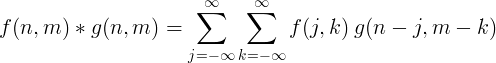
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Ми можемо відфільтрувати дискретний вхідний сигнал x (n) за допомогою згортки з імпульсною характеристикою h (n), щоб отримати вихідний сигнал y (n).

y ( n ) = x ( n ) * h ( n )

Перетворення Фур'є множення 2-х функцій дорівнює згортці перетворень Фур'є кожної функції:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Перетворення Фур'є згортки 2-х функцій дорівнює множенню перетворень Фур'є кожної функції:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Дивіться також