قدرتی لوگاریتم - ایل این (ایکس)

قدرتی لوگارڈم ایک عدد کی بیس ای پر لاگ ان گار ہے۔

قدرتی لوگرتھم کی تعریف

کب

e y = x

پھر بیس اور x کا لوگرتھم ہے

ln ( x ) = لاگ ای ( x ) = y

 

ای مسلسل یا عائلر کی تعداد ہے:

ای ≈ 2.71828183

L3 لاتعلقی فعل کے الٹا فعل کے طور پر

قدرتی لوگارڈم فنکشن ایل این (ایکس) مفاصلہ فنکشن ای ایکس کا الٹا کام ہے ۔

x/ 0 کے لئے ،

f ( f -1 ( x )) = e ln ( x ) = x

یا

f -1 ( f ( x )) = ln ( ای x ) = x

قدرتی لوگاردھم کے اصول اور خواص

اصول نام قاعدہ مثال
مصنوع کا قاعدہ

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
قارئین اصول

ln ( x / y ) = ln ( x ) - ln ( y )

LN (3 / 7) = LN (3) - LN (7)
طاقت کا قاعدہ

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
LN مشتق
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
LN لازمی
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
منفی تعداد کا LN
 جب x ≤ 0 ہوتا ہے تو ln ( x ) کی وضاحت نہیں کی جاتی ہے  
صفر کے LN
 ln (0) غیر متعینہ ہے  
 
ایک کے LN
 ln (1) = 0  
لامحدودیت
 لم ln ( x ) = ∞ ، جب x → ∞  
یولر کی شناخت ln (-1) = i π  

 

لوگرتھم پروڈکٹ رول

x اور y کے ضرب کا لوگرتھم x اور y کے لوگرتھم کا جوڑا ہے۔

لاگ بی ( x ∙ y ) = لاگ ب ( ایکس ) + لاگ ب ( و )

مثال کے طور پر:

لاگ 10 (3 ∙ 7) = لاگ 10 (3) + لاگ 10 (7)

لوگریتھم قابلیت کا قاعدہ

x اور y کے تقسیم کا لوگاریتم x اور y کے لوگارتھم کا فرق ہے۔

لاگ b ( x / y ) = لاگ b ( x ) - لاگ b ( y )

مثال کے طور پر:

لاگ ان کریں 10 (3 / 7) = لاگ ان کریں 10 (3) - لاگ ان کریں 10 (7)

لوگرتھم پاور رول

y کی طاقت میں اٹھائے جانے والے x کا لوگرتھم x کے لوگاریتم سے y گنا ہے۔

لاگ بی ( x y ) = y ∙ لاگ ب ( ایکس )

مثال کے طور پر:

لاگ 10 (2 8 ) = 8 ∙ لاگ 10 (2)

قدرتی لوگارڈم سے ماخوذ

قدرتی لوگارڈم فنکشن کا مشتق ایک دوسرے سے متعلق فعل ہے۔

کب

f ( x ) = ln ( x )

F (x) کا مشتق ہے:

f ' ( x ) = 1 / x

قدرتی لوگیٹریم کا انضمام

قدرتی لوگارڈم فنکشن کا لازمی جزو اس کے ذریعہ دیا گیا ہے:

کب

f ( x ) = ln ( x )

f (x) کا لازمی حصہ یہ ہے:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

0 کا Ln

قدرتی لوگرتھم صفر کی وضاحت نہیں کی گئی ہے۔

ln (0) غیر متعینہ ہے

x کے قدرتی لوگرتھم کے قریب 0 کی حد ، جب ایکس صفر کے قریب آجاتا ہے تو ، منفی انفینٹی ہے:

1 کے Ln

کسی کا قدرتی لوگارٹم صفر ہے:

ln (1) = 0

لامحدودیت

فطرت لافیتھم آف انفینٹی کی حد ، جب ایکس لامحدود تک پہنچ جاتا ہے تو لامحدود ہے:

لم ln ( x ) = ∞ ، جب x → ∞

پیچیدہ لوگرتھم

پیچیدہ نمبر z کے لئے:

z = re iθ = x + iy

پیچیدہ لوگاریتم (n = ...- 2، -1،0،1،2، ...) ہوگا:

لاگ z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · آرکٹان ( y / x ))

ایل این (X) کا گراف

x کی حقیقی غیر مثبت اقدار کے ل l ln (x) کی وضاحت نہیں کی گئی ہے۔

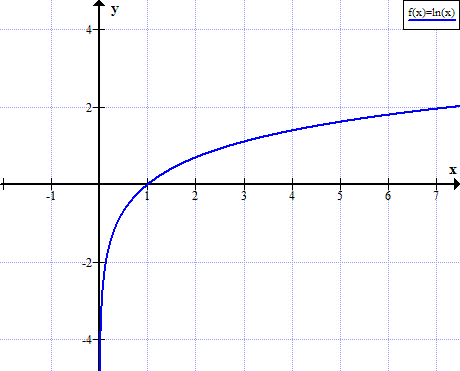
قدرتی لوگارٹم میز

x ln x
0 غیر متعینہ
0 + - ∞
0.0001 -9.210340
0.001 -6.907755
0.01 -4.605170
0.1 -2.302585
1 0
2 0.693147
ای ≈ 2.7183 1
3 1.098612
4 1.386294
5 1.609438
6 1.791759
7 1.945910
8 2.079442
9 2.197225
10 2.302585
20 2.995732
30 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6.551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

لوگرتھم کے قواعد ►

 

بھی دیکھو

الجبرا
ریپڈ ٹیبلیاں