ای مستقل

ای مستقل یا یولر کی تعداد ایک ریاضیاتی مستقل ہے۔ ای مستقل حقیقی اور غیر معقول تعداد ہے۔

ای = 2.718281828459 ...

ای کی تعریف
ای کی خصوصیات
بیس ای لوگرتھم
صریح فنکشن
یئولر کا فارمولا

ای کی تعریف

ای مستقل کی حد کے طور پر تعریف کی گئی ہے:

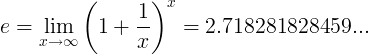
$e = \ lim_ {x \ rightarrow \ infty} \ بائیں (1+ \ frac {1} {x} \ دائیں) ^ x = 2.718281828459 ...$

متبادل تعریفیں

ای مستقل کی حد کے طور پر تعریف کی گئی ہے:

$e = \ lim_ {x \ رائٹرو 0} \ بائیں (1+ \ دائیں x) ^ rac frac {1} {x}$

ای مستقل کی وضاحت لامحدود سیریز کے طور پر کی گئی ہے۔

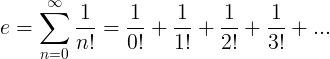
$e = \ sum_ {n = 0} ^ {\ infty} rac frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ frac {1} {3!} + ...$

ای کی خصوصیات

ای کا باہمی تعلق

ای کے تبادلے کی حد ہے:

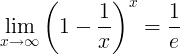
$\ لم_ {x \ رائٹیرو \ انفٹی} \ بائیں (1- \ frac {1} {x} \ دائیں) ^ x = \ frac {1} {e}$

ای کے مشتق

مصافاتی فعل کا مشتق صریح فعل ہے:

( ای ^ایکس ) '= ای ^ایکس

قدرتی لوگارڈم فنکشن کا مشتق ایک دوسرے سے متعلق فعل ہے:

(لاگ _ای ایکس ) '= (ایل این ایکس )' = 1 / ایکس

ای کے انضمام

اسی دالہ e کی غیر معینہ لازمی ^X اسی دالہ e ہے ^ایکس .

∫ ای ^ایکس DX = ای ^ایکس + C

قدرتی لوگارڈم فنکشن لاگ _ای ایکس کا غیر معینہ مدت تک لازمی عنصر یہ ہے:

∫ لاگ _ای x dx = ∫ ln x dx = x ln x - x + c

باہمی فعل 1 / x کے 1 سے e تک کے آخری جزو 1 ہیں:

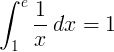
$_ int_ {1} ^ {e} rac frac {1} {x} \: dx = 1$

بیس ای لوگرتھم

ایک نمبر x کے قدرتی لوگارڈم کو x کے بیس اور لوگارڈم سے تعبیر کیا گیا ہے:

ln x = لاگ _ای x

صریح فنکشن

مصافاتی فعل کی وضاحت اس طرح کی گئی ہے:

f ( x ) = exp ( x ) = e ^x

یئولر کا فارمولا

مختلط عدد ای ^iθ شناخت ہے:

e ^iθ = cos ( θ ) + میں گناہ ( θ )

میں خیالی یونٹ (-1 کا مربع جڑ) ہے۔

any کوئی حقیقی تعداد ہے۔