Phương trình bậc hai
Phương trình bậc hai là một đa thức bậc hai với 3 hệ số - a , b , c .
Phương trình bậc hai được cho bởi:
ax 2 + bx + c = 0
Nghiệm của phương trình bậc hai được cho bởi 2 số x 1 và x 2 .
Ta có thể đổi phương trình bậc hai về dạng:
( x - x 1 ) ( x - x 2 ) = 0
Công thức phương trình bậc hai
Nghiệm của phương trình bậc hai được cho bởi công thức bậc hai:
![]()
Biểu thức bên trong căn bậc hai được gọi là phân biệt và được ký hiệu là Δ:
Δ = b 2 - 4 ac
Công thức bậc hai với ký hiệu phân biệt:
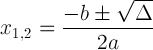
Biểu thức này rất quan trọng vì nó có thể cho chúng ta biết về giải pháp:
- Khi Δ/ 0, có 2 nghiệm thực x 1 = (- b + √ Δ ) / (2a) và x 2 = (- b-√ Δ ) / (2a) .
- Khi Δ = 0, có một nghiệm nguyên x 1 = x 2 = -b / (2a) .
- Khi Δ <0 thì không có căn thực nào tồn tại 2 căn phức:
x 1 = (- b + i√ -Δ ) / (2a) và x 2 = (- bi√ -Δ ) / (2a) .
Vấn đề số 1
3 x 2 +5 x +2 = 0
giải pháp:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Vấn đề số 2
3 x 2 -6 x +3 = 0
giải pháp:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Vấn đề số 3
x 2 +2 x +5 = 0
giải pháp:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Không có giải pháp thực sự. Các giá trị là số phức:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Đồ thị hàm số bậc hai
Hàm bậc hai là một hàm đa thức bậc hai:
f ( x ) = ax 2 + bx + c
Các nghiệm của phương trình bậc hai là nghiệm của hàm số bậc hai, là giao điểm của đồ thị hàm số bậc hai với trục x, khi
f ( x ) = 0
Khi có 2 giao điểm của đồ thị với trục x thì có 2 nghiệm của phương trình bậc hai.
Khi có 1 giao điểm của đồ thị với trục x thì có 1 nghiệm của phương trình bậc hai.
Khi không có giao điểm nào của đồ thị với trục x, ta nhận được không phải là nghiệm thực (hoặc 2 nghiệm phức).