Logarit tự nhiên - ln (x)

Lôgarit tự nhiên là lôgarit đến cơ số e của một số.

Định nghĩa lôgarit tự nhiên

Khi nào

e y = x

Khi đó logarit cơ số e của x là

ln ( x ) = log e ( x ) = y

 

Các e thường xuyên hoặc số Euler là:

e ≈ 2.71828183

Ln là hàm ngược của hàm mũ

Hàm logarit tự nhiên ln (x) là hàm ngược của hàm mũ e x .

Đối với x/ 0,

f ( f -1 ( x )) = e ln ( x ) = x

Hoặc

f -1 ( f ( x )) = ln ( e x ) = x

Các quy tắc và tính chất lôgarit tự nhiên

Tên quy tắc Qui định Thí dụ
Quy tắc nhân

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
Quy tắc thương số

ln ( x / y ) = ln ( x ) - ln ( y )

ln (3 / 7) = ln (3) - ln (7)
Quy tắc quyền lực

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
đạo hàm ln
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
tích phân ln
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
ln của số âm
 ln ( x ) không xác định khi x ≤ 0  
bằng 0
 ln (0) là không xác định  
 
Trong một
 ln (1) = 0  
trong vô cực
 lim ln ( x ) = ∞, khi x → ∞  
Danh tính của Euler ln (-1) = i π  

 

Quy tắc tích lôgarit

Lôgarit của phép nhân x và y là tổng lôgarit của x và lôgarit của y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Ví dụ:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Quy tắc thương số lôgarit

Logarit của phép chia x và y là hiệu của logarit của x và logarit của y.

log b ( x / y ) = log b ( x ) - log b ( y )

Ví dụ:

log 10 (3 / 7) = log 10 (3) - log 10 (7)

Quy tắc lũy thừa lôgarit

Lôgarit của x được nâng lên thành lũy thừa của y là y nhân với lôgarit của x.

log b ( x y ) = y ∙ log b ( x )

Ví dụ:

log 10 (2 8 ) = 8 ∙ log 10 (2)

Đạo hàm của lôgarit tự nhiên

Đạo hàm của hàm logarit tự nhiên là hàm nghịch biến.

Khi nào

f ( x ) = ln ( x )

Đạo hàm của f (x) là:

f ' ( x ) = 1 / x

Tích phân của logarit tự nhiên

Tích phân của hàm logarit tự nhiên được cho bởi:

Khi nào

f ( x ) = ln ( x )

Tích phân của f (x) là:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

Ln của 0

Lôgarit tự nhiên của 0 là không xác định:

ln (0) là không xác định

Giới hạn gần 0 của lôgarit tự nhiên của x, khi x tiếp cận 0, là trừ vô cùng:

Ln của 1

Lôgarit tự nhiên của một bằng 0:

ln (1) = 0

Ln của vô cùng

Giới hạn của lôgarit tự nhiên của vô cùng, khi x tiến tới vô cùng bằng vô cùng:

lim ln ( x ) = ∞, khi x → ∞

Lôgarit phức tạp

Đối với số phức z:

z = re iθ = x + iy

Lôgarit phức sẽ là (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

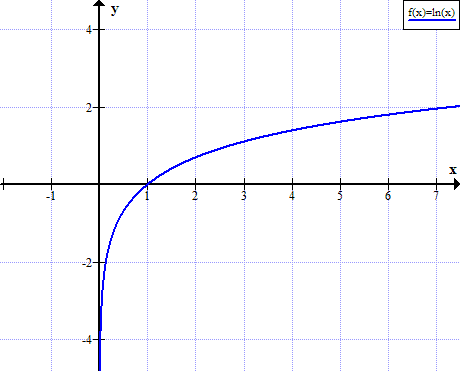
Đồ thị của ln (x)

ln (x) không được xác định cho các giá trị thực không dương của x:

Bảng logarit tự nhiên

x ln x
0 chưa xác định
0 + - ∞
0,0001 -9.210340
0,001 -6.907755
0,01 -4.605170
0,1 -2,302585
1 0
2 0,693147
e ≈ 2,7183 1
3 1,098612
4 1.386294
5 1.609438
6 1.791759
7 1.945910
8 2.079442
9 2.197225
10 2.302585
20 2.995732
30 3,401197
40 3.688879
50 3,912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6,551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

Quy tắc lôgarit ►

 

Xem thêm

ĐẠI SỐ HỌC
BẢNG RAPID