Tích phân

Tích hợp là hoạt động ngược lại của phép phái sinh.

Tích phân của một hàm số là diện tích bên dưới đồ thị của hàm số.

Định nghĩa tích phân không xác định

Khi nào dF (x) / dx = f (x) =/ tích phân (f (x) * dx) = F (x) + c

Thuộc tính tích phân không xác định

tích phân (f (x) + g (x)) * dx = tích phân (f (x) * dx) + tích phân (g (x) * dx)

tích phân (a * f (x) * dx) = a * tích phân (f (x) * dx)

tích phân (f (a * x) * dx) = 1 / a * F (a * x) + c

tích phân (f (x + b) * dx) = F (x + b) + c

tích phân (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

tích phân (df (x) / dx * dx) = f (x)

Thay đổi biến tích hợp

Khi nào x = g (t)  và dx = g '(t) * dt

tích phân (f (x) * dx) = tích phân (f (g (t)) * g '(t) * dt)

Tích hợp theo các bộ phận

tích phân (f (x) * g '(x) * dx) = f (x) * g (x) - tích phân (f' (x) * g (x) * dx)

Bảng tích phân

tích phân (f (x) * dx = F (x) + c

tích phân (a * dx) = a * x + c

tích phân (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, khi a </ - 1

tích phân (1 / x * dx) = ln (abs (x)) + c

tích phân (e ^ x * dx) = e ^ x + c

tích phân (a ^ x * dx) = a ^ x / ln (x) + c

tích phân (ln (x) * dx) = x * ln (x) - x + c

tích phân (sin (x) * dx) = -cos (x) + c

tích phân (cos (x) * dx) = sin (x) + c

tích phân (tan (x) * dx) = -ln (abs (cos (x))) + c

tích phân (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

tích phân (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

tích phân (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

tích phân (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

tích phân (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

tích phân (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

tích phân (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

tích phân (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

tích phân (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

tích phân (sinh (x) * dx) = cosh (x) + c

tích phân (cosh (x) * dx) = sinh (x) + c

tích phân (tanh (x) * dx) = ln (cosh (x)) + c

 

Định nghĩa tích phân xác định

tích phân (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)))  

Khi nào x0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Tính tích phân xác định

Khi nào  ,

  dF (x) / dx = f (x)  và

tích phân (a..b, f (x) * dx) = F (b) - F (a)  

Thuộc tính tích phân xác định

tích phân (a..b, (f (x) + g (x)) * dx) = tích phân (a..b, f (x) * dx) + tích phân (a..b, g (x) * dx )

tích phân (a..b, c * f (x) * dx) = c * tích phân (a..b, f (x) * dx)

tích phân (a..b, f (x) * dx) = - tích phân (b..a, f (x) * dx)

tích phân (a..b, f (x) * dx) = tích phân (a..c, f (x) * dx) + tích phân (c..b, f (x) * dx)

abs (tích phân (a..b, f (x) * dx)) <= tích phân (a..b, abs (f (x)) * dx)

min (f (x)) * (ba) <= tích phân (a..b, f (x) * dx) <= max (f (x)) * (ba)  khi nào x thành viên của [a, b]

Thay đổi biến tích hợp

Khi nào x = g (t)  , dx = g '(t) * dt  , g (alpha) = a  , g (beta) = b

tích phân (a..b, f (x) * dx) = tích phân (alpha..beta, f (g (t)) * g '(t) * dt)

Tích hợp theo các bộ phận

tích phân (a..b, f (x) * g '(x) * dx) = tích phân (a..b, f (x) * g (x) * dx) - tích phân (a..b, f' (x) * g (x) * dx)

Định lý giá trị trung bình

Khi f ( x ) liên tục thì có một điểm c là thành viên của [a, b]  vì thế

tích phân (a..b, f (x) * dx) = f (c) * (ba)   

Phép gần đúng hình thang của tích phân xác định

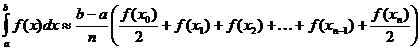
tích phân (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Hàm Gamma

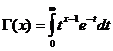
gamma (x) = tích phân (0..inf, t ^ (x-1) * e ^ (- t) * dt

Hàm Gamma là hội tụ cho x/ 0 .

Thuộc tính hàm gamma

G ( x +1) = x G ( x )

G ( n +1) = n ! , khi n ℕ (số nguyên dương). là thành viên của

Chức năng Beta

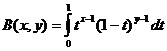
B (x, y) = tích phân (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Mối quan hệ giữa hàm Beta và hàm Gamma

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

TÍNH TOÁN
BẢNG RAPID