Phương sai

Trong xác suất và thống kê, phương sai của một biến ngẫu nhiên là giá trị trung bình của khoảng cách bình phương so với giá trị trung bình. Nó đại diện cho cách biến ngẫu nhiên được phân phối gần giá trị trung bình. Phương sai nhỏ chỉ ra rằng biến ngẫu nhiên được phân phối gần giá trị trung bình. Phương sai lớn chỉ ra rằng biến ngẫu nhiên được phân phối xa giá trị trung bình. Ví dụ, với phân phối chuẩn, đường cong hình chuông hẹp sẽ có phương sai nhỏ và đường cong hình chuông rộng sẽ có phương sai lớn.

Định nghĩa phương sai

Phương sai của biến ngẫu nhiên X là giá trị kỳ vọng của bình phương hiệu của X và giá trị kỳ vọng μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Từ định nghĩa của phương sai, chúng ta có thể nhận được

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Phương sai của biến ngẫu nhiên liên tục

Đối với biến ngẫu nhiên liên tục có giá trị trung bình μ và hàm mật độ xác suất f (x):

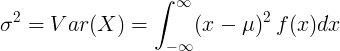
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

hoặc

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Phương sai của biến ngẫu nhiên rời rạc

Đối với biến ngẫu nhiên rời rạc X có giá trị trung bình μ và hàm khối lượng xác suất P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

hoặc

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

Thuộc tính của phương sai

Khi X và Y là các biến ngẫu nhiên độc lập:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Độ lệch chuẩn ►

 

Xem thêm

TÍNH KHẢ NĂNG & THỐNG KÊ
BẢNG RAPID