Phân phối xác suất
Trong xác suất và thống kê phân phối là một đặc trưng của một biến ngẫu nhiên, mô tả xác suất của biến ngẫu nhiên trong mỗi giá trị.
Mỗi phân phối có một hàm mật độ xác suất và hàm phân phối xác suất nhất định.
Mặc dù có số lượng phân bố xác suất không xác định, có một số phân phối phổ biến đang được sử dụng.
Chức năng phân phối tích lũy
Phân phối xác suất được mô tả bởi hàm phân phối tích lũy F (x),
là xác suất của biến ngẫu nhiên X nhận giá trị nhỏ hơn hoặc bằng x:
F ( x ) = P ( X ≤ x )
Phân phối liên tục
Hàm phân phối tích lũy F (x) được tính bằng tích phân của hàm mật độ xác suất f (u) của biến ngẫu nhiên liên tục X.
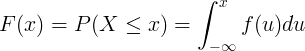
Phân phối rời rạc
Hàm phân phối tích lũy F (x) được tính bằng tổng của hàm khối lượng xác suất P (u) của biến ngẫu nhiên rời rạc X.
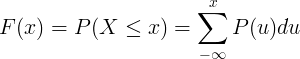
Bảng phân phối liên tục
Phân phối liên tục là phân phối của một biến ngẫu nhiên liên tục.
Ví dụ về phân phối liên tục
...
Bảng phân phối liên tục
| Tên phân phối | Ký hiệu phân phối | Hàm mật độ xác suất (pdf) | Nghĩa là | Phương sai |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Bình thường / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Đồng phục | X ~ Ư ( a , b ) |
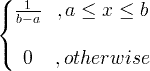 |
|
|
| số mũ | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 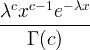 x / 0, c / 0, λ/ 0 |
|
|
| Chi vuông | X ~ χ 2 ( k ) |
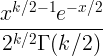 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Nhật ký bình thường | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Cơm | ||||
| Sinh viên của t |
Bảng phân phối rời rạc
Phân phối rời rạc là phân phối của một biến ngẫu nhiên rời rạc.
Ví dụ về phân phối rời rạc
...
Bảng phân phối rời rạc
| Tên phân phối | Ký hiệu phân phối | Hàm khối lượng xác suất (pmf) | Nghĩa là | Phương sai | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Nhị thức | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Đồng phục | X ~ Ư ( a, b ) |
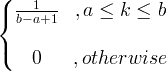 |
|
|
|
| Hình học | X ~ Geom ( p ) |
|
|
|
|
| Siêu hình học | X ~ HG ( N , K , n ) |
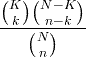 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
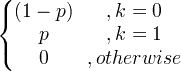 |
p |
p (1- p ) |
|
Xem thêm
TÍNH KHẢ NĂNG & THỐNG KÊ
- Xác suất cơ bản
- Sự mong đợi
- Phương sai
- Độ lệch chuẩn
- Phân phối xác suất
- Phân phối bình thường
- Ký hiệu thống kê
BẢNG RAPID