Công thức xác suất cơ bản

Phạm vi xác suất

0 ≤ P ( A ) ≤ 1

Quy tắc về sự kiện bổ sung

P ( A ^C ) + P ( A ) = 1

Quy tắc bổ sung

P (A∪B) = P (A) + P (B) - P (A∩B)

Sự kiện rời rạc

Sự kiện A và B không liên quan đến nhau

P (A∩B) = 0

Xác suất có điều kiện

P (A | B) = P (A∩B) / P (B)

Công thức Bayes

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Sự kiện độc lập

Sự kiện A và B là độc lập

P (A∩B) = P (A) ⋅ P (B)

Chức năng phân phối tích lũy

F _X ( x ) = P ( X ≤ x )

Chức năng có thể xảy ra tập trung

Hàm mật độ xác suất

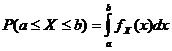
Hiệp phương sai

Tương quan

Bernoulli: 0 lần thất bại 1 lần thành công

Hình học: 0 lần thất bại 1 lần thành công

Hypergeometric: N đối tượng với K đối tượng thành công, n đối tượng được lấy.