二次方程
二次方程是二階多項式與3個係數-一個,b,c ^。
二次方程由下式給出:
斧2 + BX + C ^ = 0
二次方程的解由2個數字x 1和x 2給出。
我們可以將二次方程式更改為以下形式:
(x - x 1)(x - x 2)= 0
二次公式
二次方程的解由二次方程給出:
![]()
平方根內的表達式稱為判別式,用Δ表示:
Δ= b 2 - 4 AC
具有判別符號的二次公式:
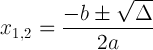
此表達式很重要,因為它可以告訴我們有關解決方案的信息:
- 當Δ/ 0時,存在2個實根x 1 =(-b + √Δ)/(2a)和x 2 =(-b- √Δ)/(2a)。
- 當Δ= 0時,存在一個根x 1 = x 2 = -b /(2a)。
- 當Δ<0時,沒有實根,則有2個複數根:
x 1 =(-b +i√- Δ)/(2a)和x 2 =(-bi√- Δ)/(2a)。
問題1
3 x 2 +5 x +2 = 0
解:
a = 3,b = 5,c = 2
X 1,2 =(-5±√(5 2 - 4×3×2))/(2×3)=(-5±√(25-24))/ 6 =(-5±1)/ 6
x 1 =(-5 + 1)/ 6 = -4/6 = -2/3
x 2 =(-5-1)/ 6 = -6/6 = -1
問題二
3 x 2 -6 x +3 = 0
解:
a = 3,b = -6,c = 3
X 1,2 =(6±√((-6)2 - 4×3×3))/(2×3)=(6±√(36-36))/ 6 =(6±0)/ 6
x 1 = x 2 = 1
問題三
x 2 +2 x +5 = 0
解:
a = 1,b = 2,c = 5
X 1,2 =(-2±√(2 2 - 4×1×5))/(2×1)=(-2±√(4-20))/ 2 =(-2±√(-16 ))/ 2
沒有真正的解決方案。這些值是複數:
x 1 = -1 + 2我
x 2 = -1-2 i
二次函數圖
二次函數是二階多項式函數:
f(x)= ax 2 + bx + c
二次方程的解是二次函數的根,即二次函數圖與x軸的交點,當
f(x)= 0
當圖形的x軸有2個交點時,二次方程有2個解。
當圖形與x軸的交點為1時,二次方程式為1。
當圖上沒有與x軸的交點時,我們將不會得到真實的解決方案(或2個複雜的解決方案)。