自然對數-ln(x)
自然對數是數字以e為底的對數。
自然對數的定義
什麼時候
Ë ÿ = X
則x的底e對數為
ln(x)=對數e(x)= y
該Ë常數或歐拉數為:
Ë ≈2.71828183
Ln是指數函數的反函數
自然對數函數ln(x)是指數函數e x的反函數。
對於x/ 0,
f(f -1(x))= e ln(x) = x
或
f -1(f(x))= ln(e x)= x
自然對數規則和屬性
| 規則名稱 | 規則 | 例 |
|---|---|---|
產品規則 |
ln(x∙y)= ln(x)+ ln(y) |
ln(3 ∙ 7)= ln(3)+ ln(7) |
商法則 |
LN(X / Y)= LN(X)- LN(Ý) |
LN(3 / 7)= LN(3)- LN(7) |
功率規則 |
ln(x y)= y∙ ln(x) |
ln(2 8)= 8 ∙ ln(2) |
ln衍生物 |
f(x)= ln(x) ⇒f '(x)= 1 / x | |
ln積分 |
∫ln (x)dx = x∙(ln(x)-1)+ C | |
負數ln |
LN(X)是未定義當 X ≤0 | |
ln為零 |
ln(0)未定義 | |
ln一 |
ln(1)= 0 | |
無限大 |
lim ln(x)=∞,當x →∞ | |
| 歐拉的身份 | LN(-1)=我π |
對數乘積規則
x和y的對數是x和y的對數之和。
log b(x∙y)= log b(x)+ log b(y)
例如:
日誌10(3 ∙ 7)=日誌10(3)+日誌10(7)
對數商法則
x和y的對數是x和y的對數之差。
日誌b(X / Y)=日誌b(X)-日誌b(Ý)
例如:
日誌10(3 / 7)=日誌10(3)-日誌10(7)
對數冪規則
x的對數提高到y的冪是y乘以x的對數。
log b(x y)= y∙ log b(x)
例如:
日誌10(2 8)= 8 ∙日誌10(2)
自然對數的導數
自然對數函數的導數是倒數函數。
什麼時候
f(x)= ln(x)
f(x)的導數為:
f'(x)= 1 / x
自然對數的積分
自然對數函數的積分由下式給出:
什麼時候
f(x)= ln(x)
f(x)的積分是:
∫ ˚F(X)DX =∫ LN(X)DX = X∙(LN(X) - 1)+ C ^
Ln為0
零的自然對數未定義:
ln(0)未定義
x接近零時,x的自然對數的接近於0的極限為負無窮大:
![]()
1的Ln
1的自然對數為零:
ln(1)= 0
無窮大
當x接近無窮大時,無窮大自然對數的極限等於無窮大:
當x →∞時lim ln(x)= ∞
複數對數
對於復數z:
z = reiθ = x + iy
複數對數為(n = ...- 2,-1,0,1,2,...):
對數z = ln(r)+ i(θ+2nπ)= ln(√(x 2 + y 2))+ i ·arctan(y / x))
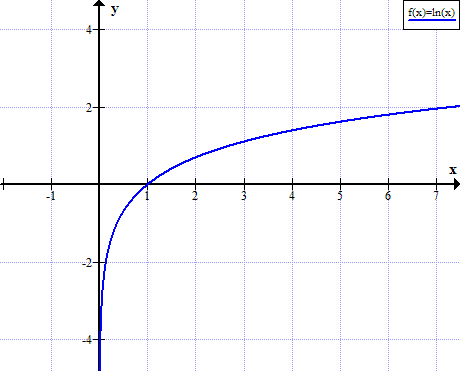
ln(x)的圖
沒有為x的實非正值定義ln(x):
自然對數表
| x | ln x |
|---|---|
| 0 | 未定義 |
| 0 + | -∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| Ë ≈2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |