方差
在概率和統計中,隨機變量的方差是與平均值的平方距離的平均值。它表示隨機變量如何在均值附近分佈。小方差表明隨機變量分佈在平均值附近。大方差表明隨機變量的分佈遠離平均值。例如,對於正態分佈,窄鐘形曲線將具有較小的方差,而寬鐘形曲線將具有較大的方差。
方差定義
隨機變量X的方差是X與期望值μ之差的平方的期望值。
σ 2 =無功(X)= È [(X - μ)2 ]
從方差的定義中我們可以得到
σ 2 =無功(X)= È(X 2) - μ 2
連續隨機變量的方差
對於具有均值μ和概率密度函數f(x)的連續隨機變量:
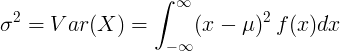
或
![Var(X)= \ left [\ int _ {-\ infty} ^ {\ infty} x ^ 2 \:f(x)dx \ right]-\ mu ^ 2](variance/cont_var2.gif)
離散隨機變量的方差
對於具有均值μ和概率質量函數P(x)的離散隨機變量X:
![]()
或
![Var(X)= \ left [\ sum_ {i} ^ {} x_i ^ 2P(x_i)\ right]-\ mu ^ 2](variance/disc_var2.gif)
方差的性質
當X和Y是獨立隨機變量時:
變量(X + Y)=變量(X)+變量(Y)