概率分佈
在概率統計中分佈是隨機變量的一個特徵,描述每個值中隨機變量的概率。
每個分佈具有一定的概率密度函數和概率分佈函數。
儘管存在不確定數量的概率分佈,但有幾種常用的分佈在使用中。
累積分佈函數
概率分佈由累積分佈函數F(x)描述,
這是隨機變量X獲得小於或等於x的值的概率:
˚F(X)= P(X ≤ X)
持續分配
通過對連續隨機變量X的概率密度函數f(u)進行積分來計算累積分佈函數F(x)。
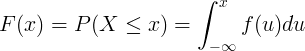
離散分佈
累積分佈函數F(x)是通過離散隨機變量X的概率質量函數P(u)的總和計算得出的。

連續分佈表
連續分佈是連續隨機變量的分佈。
連續分配示例
...
連續分佈表
| 發行名稱 | 分配符號 | 概率密度函數(pdf) | 意思 | 方差 |
|---|---|---|---|---|
| f X(x) |
μ = E(X) |
σ 2 =無功(X) |
||
| 普通/高斯 | X〜Ñ(μ,σ 2) |
|
μ | σ 2 |
| 制服 | X〜ü(一,b) |
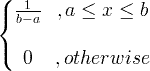 |
|
|
| 指數的 | X〜EXP(λ) | |
|
|
| 伽瑪 | X〜伽馬(Ç,λ) | 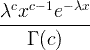 x / 0,c / 0,λ/ 0 |
|
|
| 卡方 | X〜 χ 2(ķ) |
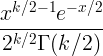 |
k |
2千 |
| 威沙特 | ||||
| F | X〜˚F(ķ 1 ,K 2) |
|||
| 貝塔 | ||||
| 威布爾 | ||||
| 對數正態 | X〜LN(μ,σ 2) |
|||
| 瑞利 | ||||
| 柯西 | ||||
| Dirichlet | ||||
| 拉普拉斯 | ||||
| 徵收 | ||||
| 白飯 | ||||
| 學生的 |
離散分佈表
離散分佈是離散隨機變量的分佈。
離散分佈示例
...
離散分佈表
| 發行名稱 | 分配符號 | 概率質量函數(pmf) | 意思 | 方差 | |
|---|---|---|---|---|---|
| f x(k)= P(X = k) k = 0,1,2,... |
E(x) | 變量(x) | |||
| 二項式 | X〜濱(Ñ,p) |
|
np |
np(1- p) |
|
| 泊松 | X〜泊松(λ) |
|
λ≥0 |
λ |
λ |
| 制服 | X〜ù(A,B) |
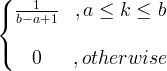 |
|
|
|
| 幾何 | X〜的Geom(p) |
|
|
|
|
| 超幾何 | X〜HG(Ñ,ķ,Ñ) |
 |
N = 0,1,2,... K = 0,1,..,N n = 0,1,...,N |
|
|
| 貝努利 | X〜伯爾尼(p) |
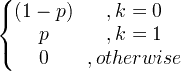 |
p |
p(1- p) |
|