معادلة من الدرجة الثانية
المعادلة التربيعية هي كثيرة الحدود من الدرجة الثانية ولها 3 معاملات - أ ، ب ، ج .
تُعطى المعادلة التربيعية بواسطة:
الفأس 2 + ب س + ج = 0
يُعطى حل المعادلة التربيعية بعدد 2 x 1 و x 2 .
يمكننا تغيير المعادلة التربيعية إلى شكل:
( س - س 1 ) ( س - س 2 ) = 0
الصيغة التربيعية
يتم الحصول على حل المعادلة التربيعية بواسطة الصيغة التربيعية:
![]()
ويطلق على التعبير داخل الجذر التربيعي التمايز ويرمز التي كتبها Δ:
Δ = ب 2 - 4 ميلان
الصيغة التربيعية مع تدوين مميز:
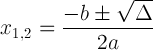
هذا التعبير مهم لأنه يخبرنا عن الحل:
- عندما تكون Δ/ 0 ، يكون هناك جذران حقيقيان x 1 = (- b + √ Δ ) / (2a) و x 2 = (- b-√ Δ ) / (2a) .
- عندما تكون Δ = 0 ، يوجد جذر واحد x 1 = x 2 = -b / (2a) .
- عندما Δ <0 لا توجد جذور حقيقية، هناك 2 جذور معقدة:
س 1 = (- ب + i√ -Δ ) / (2A) و x 2 = (- bi√ -Δ ) / (2A) .
المشكلة رقم 1
3 × 2 +5 × +2 = 0
المحلول:
أ = 3 ، ب = 5 ، ج = 2
س 1،2 = (-5 ± √ من (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
× 1 = (-5 + 1) / 6 = -4/6 = -2/3
× 2 = (-5 - 1) / 6 = -6/6 = -1
المشكلة رقم 2
3 × 2 -6 × +3 = 0
المحلول:
أ = 3 ، ب = -6 ، ج = 3
س 1،2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
س 1 = س 2 = 1
المشكلة رقم 3
س 2 + 2 س +5 = 0
المحلول:
أ = 1 ، ب = 2 ، ج = 5
س 1،2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
لا توجد حلول حقيقية. القيم هي أرقام مركبة:
س 1 = -1 + 2 ط
س 2 = -1-2 ط
الرسم البياني للوظيفة التربيعية
الوظيفة التربيعية هي دالة متعددة الحدود من الدرجة الثانية:
و ( س ) = فأس 2 + ب س + ج
حلول المعادلة التربيعية هي جذور الدالة التربيعية ، وهي نقاط تقاطع الرسم البياني للوظيفة التربيعية مع المحور x ، عندما
و ( س ) = 0
عند وجود نقطتي تقاطع للرسم البياني مع المحور x ، يكون هناك حلان للمعادلة التربيعية.
عندما يكون هناك نقطة تقاطع واحدة للرسم البياني مع المحور x ، يكون هناك حل واحد للمعادلة التربيعية.
عندما لا توجد نقاط تقاطع للرسم البياني مع المحور السيني ، لا نحصل على حل حقيقي (أو حلان معقدان).