اللوغاريتم الطبيعي - ln (x)
اللوغاريتم الطبيعي هو لوغاريتم الأساس e لرقم.
- تعريف اللوغاريتم الطبيعي (ln)
- قواعد وخصائص اللوغاريتم الطبيعي (ln)
- لوغاريتم معقد
- رسم بياني لـ ln (x)
- جدول اللوغاريتمات الطبيعية (ln)
- حاسبة اللوغاريتم الطبيعي
تعريف اللوغاريتم الطبيعي
متى
ه ذ = س
إذن ، لوغاريتم الأساس e لـ x هو
ln ( x ) = log e ( x ) = y
و ثابت البريد أو رقم أويلر هو:
ه ≈ 2.71828183
Ln كدالة عكسية للدالة الأسية
دالة اللوغاريتم الطبيعي ln (x) هي الدالة العكسية للدالة الأسية e x .
بالنسبة إلى x/ 0 ،
f ( f -1 ( x )) = e ln ( x ) = x
أو
f -1 ( f ( x )) = ln ( e x ) = x
قواعد وخصائص اللوغاريتم الطبيعي
| اسم القاعدة | قاعدة | مثال |
|---|---|---|
سيادة المنتج |
ln ( x y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
قاعدة الحاصل |
ln ( x / y ) = ln ( x ) - ln ( y ) |
قانون الجنسية (3 / 7) = من قانون الجنسية (3) - قانون الجنسية (7) |
حكم القوة |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
مشتق ln |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
لا يتجزأ |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln للرقم السالب |
ln ( x ) غير معرف عندما x ≤ 0 | |
ln من الصفر |
ln (0) غير معرف | |
في واحد |
ln (1) = 0 | |
ln اللانهاية |
lim ln ( x ) = ، عندما x → ∞ | |
| هوية أويلر | ln (-1) = أنا π |
قاعدة منتج اللوغاريتم
لوغاريتم ضرب x و y هو مجموع لوغاريتم x ولوغاريتم y.
السجل ب ( س ∙ ص ) = السجل ب ( س ) + السجل ب ( ص )
فمثلا:
تسجيل 10 (3 ∙ 7) = تسجيل 10 (3) + تسجيل 10 (7)
قاعدة حاصل قسمة اللوغاريتم
لوغاريتم قسمة x و y هو الفرق في لوغاريتم x ولوغاريتم y.
السجل ب ( س / ص ) = السجل ب ( س ) - السجل ب ( ص )
فمثلا:
تسجيل 10 (3 / 7) = تسجيل 10 (3) - تسجيل 10 (7)
حكم قوة اللوغاريتم
لوغاريتم x مرفوع للقوة y يساوي y ضرب لوغاريتم x.
سجل ب ( س ص ) = ص ∙ سجل ب ( س )
فمثلا:
سجل 10 (2 8 ) = 8 ∙ سجل 10 (2)
مشتق من اللوغاريتم الطبيعي
مشتق دالة اللوغاريتم الطبيعي هو دالة متبادلة.
متى
و ( س ) = ن ( س )
مشتق f (x) هو:
و ' ( س ) = 1 / س
تكامل اللوغاريتم الطبيعي
يتم إعطاء تكامل دالة اللوغاريتم الطبيعي من خلال:
متى
و ( س ) = ن ( س )
تكامل f (x) هو:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln من 0
اللوغاريتم الطبيعي للصفر غير معرف:
ln (0) غير معرف
الحد القريب من 0 للوغاريتم الطبيعي لـ x ، عندما يقترب x من الصفر ، يكون سالب ما لا نهاية:
![]()
Ln من 1
اللوغاريتم الطبيعي للواحد هو صفر:
ln (1) = 0
Ln من اللانهاية
حد اللوغاريتم الطبيعي لما لا نهاية ، عندما يقترب x من اللانهاية ، يساوي اللانهاية:
lim ln ( x ) = ، عندما x → ∞
لوغاريتم معقد
للعدد المركب z:
z = re iθ = x + iy
سيكون اللوغاريتم المعقد (n = ...- 2، -1،0،1،2، ...):
السجل z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
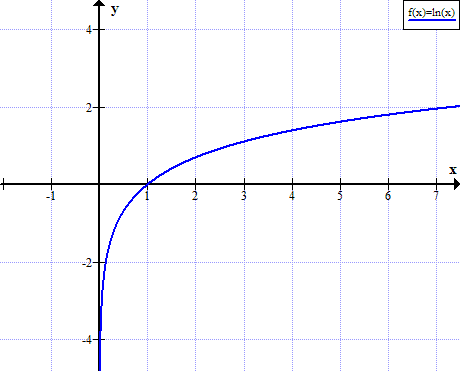
رسم بياني لـ ln (x)
لم يتم تعريف ln (x) للقيم الحقيقية غير الموجبة لـ x:
جدول اللوغاريتمات الطبيعية
| x | ln x |
|---|---|
| 0 | غير معرف |
| 0 + | - ∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| ه ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
أنظر أيضا
- لوغاريتم (سجل)
- حاسبة اللوغاريتم الطبيعي
- اللوغاريتم الطبيعي للصفر
- اللوغاريتم الطبيعي للواحد
- اللوغاريتم الطبيعي لـ e
- اللوغاريتم الطبيعي لما لا نهاية
- اللوغاريتم الطبيعي للرقم السالب
- دالة عكسية Ln
- الرسم البياني ln (x)
- جدول اللوغاريتم الطبيعي
- حاسبة اللوغاريتم
- ثابت البريد
الجبر
جداول سريعة